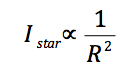
When learning the evidence best explained by the Big Bang, usually the standard pieces of observational data that are suggested include:
(1)The Cosmic Microwave Background – the remnant heat.
(2)The Hubble Expansion – the fact galaxies are moving away from each other
(3)Big Bang Nucleosynthesis - the relative abundances of light nuclei.
However, an important consideration should be the fact that the sky is dark. This simple fact – that when the sun goes down; the sky darkens, is an observation that verifies the big bang as true. The reason the sky is dark is because the universe is bounded both in space and in time. The best explanation for a dark sky seems to be that the universe cannot have existed forever and it cannot be infinitely large if the cosmological principal holds. For an infinitely old, infinitely large universe which is both homogenous and isotropic would mean that no matter where we looked, we would see photons from starlight steaming towards us and this should mean that the night sky is bright. But it is not, so the universe must be bounded in some way.
The History
Olbers’ paradox is named after Heinrich Wilhelm Olbers who presented the not-too-original argument that the night sky should be bright in a paper published in 1826. Kepler, de Chesaux and Halley had already suggested this – Kepler somewhere around 1610 in Conversations with the Starry Messenger where he said that “...in an infinite Universe the stars would fill the heavens as seen by us...” (1) and de Chessaux in the 18th century (2). Halley will be discussed later. Their belief was that the universe was infinite in size and the distribution of stars was uniform. These, for the time were reasonable assumptions however they led to false conclusions. The argument seemed to run thus:
Premise 1: The universe is filled uniformly with stars.
Premise 2: Each star gives out light.
Premise 3: The universe is infinite in size.
Conclusion: Therefore the universe should be infinite in its brightness.
Philosophically speaking, though the argument is valid, it is not sound: that is, although the form of the argument is fine, the premises are wanting for we know the conclusion is false. Either one or both of the premises are false or there are hidden assumptions.
Even without resorting to 21st century cosmological arguments, Olbers can be answered in a variety of ways. A superficially plausible, but ultimately flawed way of answering Olbers that I have not seen in the literature, would be to use a mathematical argument. It seems to me that in some ways Olbers’ Paradox is very Zeno-like in form. Indeed the word “paradox” itself comes from the Greek “paradoxo”, used in Plato's Parmenides by the Greek philosopher Zeno of Elea, who lived around 490-430 BC. The word then was used to describe some propositions put forward by Zeno which have become famous in philosophical circles today as “Zeno's paradoxes”. A form of one of Zeno’s paradoxes is the “dichotomy paradox” – which says you cannot (for example) pick up your pen, for to do so means you must first travel half the distance. But to travel half the distance you must first travel one quarter the distance, and so on ad infinitum. Therefore, because you must travel ½ + ¼ + 1/8 + … an infinite number of steps, you will never be able to pick up your pen.
However, the misconception here is that we cannot sum an infinite series and not get infinity. Infact ½ + ¼ + 1/8 +…. = 1. Such similar reasoning could possibly be applied to Olbers’ Paradox. If we assume a uniform distribution of stars, then as the distance from Earth increases, the brightness of the light from distant stars will decrease to a vanishingly small degree. Adding up the light from these stars can therefore be considered the sum of an infinite series. But the sum of an infinite series with a common ratio less than 1 will not be infinity, but rather some integer less than this. Though at first look this resolution may seem plausible, it does not stack up. The analogy with Zeno’s paradox falls down because the sum of the light from stars at increasing distance from Earth does not become vanishingly dim. Halley pointed out in 1721 (over 100 years before Olbers) (3) that in a universe with a homogenous distribution of stars, the number of stars, N, occupying the shell of a sphere of thickness T, at a radius R from the Earth’s surface would increase with increasing R. Or quantitatively:
N ∝ R^2
The further one travels away from the Earth, the more stars there are within the shell, and so at any distance although the brightness from individual stars may decrease due to distance this is balanced by an increase in the total number of stars at that distance.
Indeed at a distance R from the Earth, the intensity of light from an individual star I, is proportional to 1/R^2. That is:
In short, the sum of light will still be infinite. One way to see this is each "shell" of radius "R" contains some stars that contribute some intensity of light "I". There are an infinite number of such shells in an infinite universe and so to first approximation we expect an infinitely bright sky. Other, superior analyses will be discussed in what is to follow!
Most often the paradox is stated simply by saying that in a homogenous isotropic universe (i.e: one that obeys the cosmological principle) of infinite size, any line of sight will eventually terminate at the surface of a star. Now whether this means the sky will be infinitely bright or simply just ‘bright’ is an interesting point of discussion in itself. One may firstly assume an arbitrary brightness for a typical star. Now even if there are infinite stars in the universe and all lines of sight end upon the surface of a star, the star upon which the line of sight terminates blocks the light from stars behind it. This means that the sky need not be infinitely bright, even if there are an infinite number of stars, as stars themselves are opaque. On the other hand, for a universe that is both infinite in size and which has always existed, thermodynamics would demand that over time even the radiation from the stars behind the ones we can see would be absorbed and then re emitted causing, perhaps, infinite brightness anyway. The ‘absorption by intervening stars’ counter argument seems flawed in the sense that there are an infinite number of stars that (effectively) are transmitting photons to the star which is in the direct line of sight with the Earth. In other words the total amount of absorption occurring in the system due to an infinite number of stars must be infinite and so (therefore) according to thermodynamics, must be the level of emission (in effect the “obscuring” stars are acting just like interstellar dust, proposed as one of the solutions to Olbers’ paradox to be discussed later). This idea of intervening stars in an infinite universe not actually obscuring the radiation from more distant stars was first suggested by J. Herschel in 1848 (4).
Whatever the case, the fact remains that the night sky is not even bright let alone infinitely bright and the most obvious way to solve the paradox is simply to point out that although the cosmological principal is more or less true (the universe does look the same in all directions (however walls, voids and filaments seem to suggest that the distribution of galaxies is not completely uniform)), the universe is not infinite in size. We know, from our best theory explaining the origin of the universe, that the universe is bounded in time and space. The universe began in a hot big bang some 13.7 billion years ago and so it does not contain an infinite number of stars. However, at the time of Olbers, the Big Bang was not understood and it seemed reasonable to believe in a static, infinite universe. So how was the paradox resolved then?
18th Century Resolutions
The first is a solution provided by Halley. He basically denied the validity of the inverse square law for the intensity of light over vast distances. He believed that eventually the effective intensity of light coming from stars at a great distance from the Earth could be regarded as zero beyond a certain limit. This explained the dark night sky.
The second solution, proposed by Cheseaux in 1744, and by Heinrich Olbers himself in 1823 was that the light is absorbed by interstellar dust. As said, John Herschel explained that the thermodynamics of the situation demands the dust heat up until it emitted as much light as it absorbed; at least in an infinitely old universe.
Another solution is that although the universe may be infinite in size, it may nonetheless be finite in age. Thus, if the universe is nothing but 4,000 years old (a reasonable assumption for Christian scientists), then light at a distance of 4000+ light years could not possibly have reached us yet.
A solution, suggested by the author, consistent with the paradox is that the universe may be infinitely large and infinitely old, but that stars have a finite age. If this is the case, the infinite universe could contain a uniform distribution of brown dwarves. The bright stars we see are the exception rather than the rule. This solution could surely be a solution acceptable to 18th century astronomers. Today we see little evidence (yet!) of sufficiently large populations of dead stars however.
These older solutions to the paradox are to be found wanting today given our best description of how the universe is. Halley’s proposition of a varying inverse law to light seems very ad-hoc. It seems to be proposed as a solution to a problem with no real explanation of why it should occur. In the author’s opinion, the MOdified Newtonian Dynamics (MOND) theory of gravity presented as an alternative to ‘dark matter’ seems to be in this class of theories: an ad hoc alteration to a good theory designed simply to ‘explain away’ an observation that seems difficult. In this case, both MOND and Halley’s law for light are both minor changes to inverse square laws designed to change the way the laws of physics work over vast distances. The physical explanation seems to consist of little more than “it fits the data”.
We now also know, according to the best observational data from COBE and WMAP, for example, that the cosmic microwave background constrains the age of the universe to somewhere around 13.7 billion years old. Now, given inflation – a period of vast expansion in which space increased in volume faster than the speed of light – there may be stars that exist that we cannot see. In other words, the universe has a radius greater than 13.7 billion light years. Indeed, given the Hubble expansion, we know this is true: so there are stars whose light has not yet reached us. So on the surface, the finite age of the universe may at least go part of the way to solving Olbers’ paradox, but it is not the full story. Modern resolutions require modern cosmology.
Modern Resolutions
Olbers’ paradox suggests that the universe should be bright at night. However, this statement contains the hidden assumption that we are talking about the visible band of electromagnetic radiation. In an expanding universe, light is red shifted. Furthermore, Hubble’s law in qualitative form says that the further a light source is from the observer, the faster it appears to be receding. This means that very distant galaxies, however numerous, would have the emission of the light lengthened into the sub-red wavelengths and thus be invisible to the naked eye. This solution can also accommodate an ‘infinite’ number of stars: if the light from those stars is all red shifted beyond visible wavelengths, the sky could still be dark to human eyes. In some sense though, this is putting the cart before the horse, as the explanation of the Hubble Expansion is that the universe has a beginning and was once of zero (or at least of infinitesimally small) size. Today, the expanding universe, however large, is not infinite…and so we need not try to explain why an infinity of stars in the universe does not result in an infinitely bright sky, by using arguments about the Hubble Expansion. Such an argument seems to the author to be redundant.
General relativity predicts an expanding universe. Only by introducing a very contrived fudge factor – the original cosmological constant, can a static universe be ‘predicted’ using the equations of general relativity. An expanding universe implies an infinitesimally smaller universe in the past and hence, even in the absence of other evidence such as the abundance of light elements and the cosmic microwave background, the big bang is the best explanation for a universe consistent with general relativity. This then is both the most basic and best resolution of the paradox. General relativity goes some way to explaining why we believe the universe has not existed forever: that its age is finite – and this fact alone is sufficient to explain why the sky is dark even if the universe was (or is!) infinite in size. An infinitely old universe that is finite in size would have collapsed under its own gravity long ago, and so this cannot be a possible universe in which we live. On the other hand, a universe infinite in size, but finite in age is also unlikely given that the reason we believe in a universe of finite age is based upon a universe that was much smaller in the past. A universe that was finite in size in the past cannot become infinite in size in any finite amount of time. The best current estimate of the age of the universe is somewhere in the region of 13.4 billion years old (5), then any stars further than this away cannot yet be seen from Earth. This would be true even if a universe with a finite age had an infinite expanse. This limit of seeing is called the cosmic particle horizon and the entire observable universe is located inside this sphere (6). A second effect also contributes to the darkness of the sky and that is the Hubble expansion causing the red shift of starlight from distant galaxies. A galaxy close to the cosmic particle horizon has a redshift, z à . Therefore, the prediction from general relativity that expanding space will redshift light from distant sources suggests that the light from those stellar light sources has such low intensity it does not contribute to the brightness of the night sky in the visible band – indeed, of course, this will be true of any star whose distance from Earth is sufficient enough to redshift its light into the non-visible wavelengths.
Conclusions
One does not need to resort to the finer details of modern cosmology in order to answer Olbers. It is sufficient to state that the universe has not existed forever. However, the fact that general relativity predicts an expanding universe – a fact verified by observation of the redshift of distant galaxies – adds further weight to the solution that an infinitely bright sky cannot result from the universe in which we find ourselves. Although the redshift of distant stars is considered to be a secondary effect, the main reason the sky is dark at night is because the universe is of a finite age and so only a finite number of stars contribute to the intensity of light at night. Any other stars that may exist are beyond the cosmic particle horizon.
(1) Swinburne University of Technology CD-ROM PowerPoint m17a01 slide 6.
(2) “Encyclopedia of Astrobiology, Astronomy & Spaceflight home page” Darling, D. http://www.daviddarling.info/encyclopedia/O/Olbers_Paradox.html
(3) Swinburne University of Technology CD-ROM PowerPoint m17a01 slide 7.
(4) Arpino, M. & Scardigli, F. “Inferences from the dark sky: Olbers’ paradox revisited (2002). http://xxx.lanl.gov/pdf/astro-ph/0007428
(4) Wikipedia Olbers’ Paradox Reference http://en.wikipedia.org/wiki/Olber%27s_paradox
(5) Lineweaver, C. A Younger Age for the Universe: Science, May 28, 1999, vol 284, 1503-1507
(6) Freedman, R. & Kaufmann, W. Universe, 6th Edition Freeman, 2002
(1)The Cosmic Microwave Background – the remnant heat.
(2)The Hubble Expansion – the fact galaxies are moving away from each other
(3)Big Bang Nucleosynthesis - the relative abundances of light nuclei.
However, an important consideration should be the fact that the sky is dark. This simple fact – that when the sun goes down; the sky darkens, is an observation that verifies the big bang as true. The reason the sky is dark is because the universe is bounded both in space and in time. The best explanation for a dark sky seems to be that the universe cannot have existed forever and it cannot be infinitely large if the cosmological principal holds. For an infinitely old, infinitely large universe which is both homogenous and isotropic would mean that no matter where we looked, we would see photons from starlight steaming towards us and this should mean that the night sky is bright. But it is not, so the universe must be bounded in some way.
The History
Olbers’ paradox is named after Heinrich Wilhelm Olbers who presented the not-too-original argument that the night sky should be bright in a paper published in 1826. Kepler, de Chesaux and Halley had already suggested this – Kepler somewhere around 1610 in Conversations with the Starry Messenger where he said that “...in an infinite Universe the stars would fill the heavens as seen by us...” (1) and de Chessaux in the 18th century (2). Halley will be discussed later. Their belief was that the universe was infinite in size and the distribution of stars was uniform. These, for the time were reasonable assumptions however they led to false conclusions. The argument seemed to run thus:
Premise 1: The universe is filled uniformly with stars.
Premise 2: Each star gives out light.
Premise 3: The universe is infinite in size.
Conclusion: Therefore the universe should be infinite in its brightness.
Philosophically speaking, though the argument is valid, it is not sound: that is, although the form of the argument is fine, the premises are wanting for we know the conclusion is false. Either one or both of the premises are false or there are hidden assumptions.
Even without resorting to 21st century cosmological arguments, Olbers can be answered in a variety of ways. A superficially plausible, but ultimately flawed way of answering Olbers that I have not seen in the literature, would be to use a mathematical argument. It seems to me that in some ways Olbers’ Paradox is very Zeno-like in form. Indeed the word “paradox” itself comes from the Greek “paradoxo”, used in Plato's Parmenides by the Greek philosopher Zeno of Elea, who lived around 490-430 BC. The word then was used to describe some propositions put forward by Zeno which have become famous in philosophical circles today as “Zeno's paradoxes”. A form of one of Zeno’s paradoxes is the “dichotomy paradox” – which says you cannot (for example) pick up your pen, for to do so means you must first travel half the distance. But to travel half the distance you must first travel one quarter the distance, and so on ad infinitum. Therefore, because you must travel ½ + ¼ + 1/8 + … an infinite number of steps, you will never be able to pick up your pen.
However, the misconception here is that we cannot sum an infinite series and not get infinity. Infact ½ + ¼ + 1/8 +…. = 1. Such similar reasoning could possibly be applied to Olbers’ Paradox. If we assume a uniform distribution of stars, then as the distance from Earth increases, the brightness of the light from distant stars will decrease to a vanishingly small degree. Adding up the light from these stars can therefore be considered the sum of an infinite series. But the sum of an infinite series with a common ratio less than 1 will not be infinity, but rather some integer less than this. Though at first look this resolution may seem plausible, it does not stack up. The analogy with Zeno’s paradox falls down because the sum of the light from stars at increasing distance from Earth does not become vanishingly dim. Halley pointed out in 1721 (over 100 years before Olbers) (3) that in a universe with a homogenous distribution of stars, the number of stars, N, occupying the shell of a sphere of thickness T, at a radius R from the Earth’s surface would increase with increasing R. Or quantitatively:
N ∝ R^2
The further one travels away from the Earth, the more stars there are within the shell, and so at any distance although the brightness from individual stars may decrease due to distance this is balanced by an increase in the total number of stars at that distance.
Indeed at a distance R from the Earth, the intensity of light from an individual star I, is proportional to 1/R^2. That is:
In short, the sum of light will still be infinite. One way to see this is each "shell" of radius "R" contains some stars that contribute some intensity of light "I". There are an infinite number of such shells in an infinite universe and so to first approximation we expect an infinitely bright sky. Other, superior analyses will be discussed in what is to follow!
Most often the paradox is stated simply by saying that in a homogenous isotropic universe (i.e: one that obeys the cosmological principle) of infinite size, any line of sight will eventually terminate at the surface of a star. Now whether this means the sky will be infinitely bright or simply just ‘bright’ is an interesting point of discussion in itself. One may firstly assume an arbitrary brightness for a typical star. Now even if there are infinite stars in the universe and all lines of sight end upon the surface of a star, the star upon which the line of sight terminates blocks the light from stars behind it. This means that the sky need not be infinitely bright, even if there are an infinite number of stars, as stars themselves are opaque. On the other hand, for a universe that is both infinite in size and which has always existed, thermodynamics would demand that over time even the radiation from the stars behind the ones we can see would be absorbed and then re emitted causing, perhaps, infinite brightness anyway. The ‘absorption by intervening stars’ counter argument seems flawed in the sense that there are an infinite number of stars that (effectively) are transmitting photons to the star which is in the direct line of sight with the Earth. In other words the total amount of absorption occurring in the system due to an infinite number of stars must be infinite and so (therefore) according to thermodynamics, must be the level of emission (in effect the “obscuring” stars are acting just like interstellar dust, proposed as one of the solutions to Olbers’ paradox to be discussed later). This idea of intervening stars in an infinite universe not actually obscuring the radiation from more distant stars was first suggested by J. Herschel in 1848 (4).
Whatever the case, the fact remains that the night sky is not even bright let alone infinitely bright and the most obvious way to solve the paradox is simply to point out that although the cosmological principal is more or less true (the universe does look the same in all directions (however walls, voids and filaments seem to suggest that the distribution of galaxies is not completely uniform)), the universe is not infinite in size. We know, from our best theory explaining the origin of the universe, that the universe is bounded in time and space. The universe began in a hot big bang some 13.7 billion years ago and so it does not contain an infinite number of stars. However, at the time of Olbers, the Big Bang was not understood and it seemed reasonable to believe in a static, infinite universe. So how was the paradox resolved then?
18th Century Resolutions
The first is a solution provided by Halley. He basically denied the validity of the inverse square law for the intensity of light over vast distances. He believed that eventually the effective intensity of light coming from stars at a great distance from the Earth could be regarded as zero beyond a certain limit. This explained the dark night sky.
The second solution, proposed by Cheseaux in 1744, and by Heinrich Olbers himself in 1823 was that the light is absorbed by interstellar dust. As said, John Herschel explained that the thermodynamics of the situation demands the dust heat up until it emitted as much light as it absorbed; at least in an infinitely old universe.
Another solution is that although the universe may be infinite in size, it may nonetheless be finite in age. Thus, if the universe is nothing but 4,000 years old (a reasonable assumption for Christian scientists), then light at a distance of 4000+ light years could not possibly have reached us yet.
A solution, suggested by the author, consistent with the paradox is that the universe may be infinitely large and infinitely old, but that stars have a finite age. If this is the case, the infinite universe could contain a uniform distribution of brown dwarves. The bright stars we see are the exception rather than the rule. This solution could surely be a solution acceptable to 18th century astronomers. Today we see little evidence (yet!) of sufficiently large populations of dead stars however.
These older solutions to the paradox are to be found wanting today given our best description of how the universe is. Halley’s proposition of a varying inverse law to light seems very ad-hoc. It seems to be proposed as a solution to a problem with no real explanation of why it should occur. In the author’s opinion, the MOdified Newtonian Dynamics (MOND) theory of gravity presented as an alternative to ‘dark matter’ seems to be in this class of theories: an ad hoc alteration to a good theory designed simply to ‘explain away’ an observation that seems difficult. In this case, both MOND and Halley’s law for light are both minor changes to inverse square laws designed to change the way the laws of physics work over vast distances. The physical explanation seems to consist of little more than “it fits the data”.
We now also know, according to the best observational data from COBE and WMAP, for example, that the cosmic microwave background constrains the age of the universe to somewhere around 13.7 billion years old. Now, given inflation – a period of vast expansion in which space increased in volume faster than the speed of light – there may be stars that exist that we cannot see. In other words, the universe has a radius greater than 13.7 billion light years. Indeed, given the Hubble expansion, we know this is true: so there are stars whose light has not yet reached us. So on the surface, the finite age of the universe may at least go part of the way to solving Olbers’ paradox, but it is not the full story. Modern resolutions require modern cosmology.
Modern Resolutions
Olbers’ paradox suggests that the universe should be bright at night. However, this statement contains the hidden assumption that we are talking about the visible band of electromagnetic radiation. In an expanding universe, light is red shifted. Furthermore, Hubble’s law in qualitative form says that the further a light source is from the observer, the faster it appears to be receding. This means that very distant galaxies, however numerous, would have the emission of the light lengthened into the sub-red wavelengths and thus be invisible to the naked eye. This solution can also accommodate an ‘infinite’ number of stars: if the light from those stars is all red shifted beyond visible wavelengths, the sky could still be dark to human eyes. In some sense though, this is putting the cart before the horse, as the explanation of the Hubble Expansion is that the universe has a beginning and was once of zero (or at least of infinitesimally small) size. Today, the expanding universe, however large, is not infinite…and so we need not try to explain why an infinity of stars in the universe does not result in an infinitely bright sky, by using arguments about the Hubble Expansion. Such an argument seems to the author to be redundant.
General relativity predicts an expanding universe. Only by introducing a very contrived fudge factor – the original cosmological constant, can a static universe be ‘predicted’ using the equations of general relativity. An expanding universe implies an infinitesimally smaller universe in the past and hence, even in the absence of other evidence such as the abundance of light elements and the cosmic microwave background, the big bang is the best explanation for a universe consistent with general relativity. This then is both the most basic and best resolution of the paradox. General relativity goes some way to explaining why we believe the universe has not existed forever: that its age is finite – and this fact alone is sufficient to explain why the sky is dark even if the universe was (or is!) infinite in size. An infinitely old universe that is finite in size would have collapsed under its own gravity long ago, and so this cannot be a possible universe in which we live. On the other hand, a universe infinite in size, but finite in age is also unlikely given that the reason we believe in a universe of finite age is based upon a universe that was much smaller in the past. A universe that was finite in size in the past cannot become infinite in size in any finite amount of time. The best current estimate of the age of the universe is somewhere in the region of 13.4 billion years old (5), then any stars further than this away cannot yet be seen from Earth. This would be true even if a universe with a finite age had an infinite expanse. This limit of seeing is called the cosmic particle horizon and the entire observable universe is located inside this sphere (6). A second effect also contributes to the darkness of the sky and that is the Hubble expansion causing the red shift of starlight from distant galaxies. A galaxy close to the cosmic particle horizon has a redshift, z à . Therefore, the prediction from general relativity that expanding space will redshift light from distant sources suggests that the light from those stellar light sources has such low intensity it does not contribute to the brightness of the night sky in the visible band – indeed, of course, this will be true of any star whose distance from Earth is sufficient enough to redshift its light into the non-visible wavelengths.
Conclusions
One does not need to resort to the finer details of modern cosmology in order to answer Olbers. It is sufficient to state that the universe has not existed forever. However, the fact that general relativity predicts an expanding universe – a fact verified by observation of the redshift of distant galaxies – adds further weight to the solution that an infinitely bright sky cannot result from the universe in which we find ourselves. Although the redshift of distant stars is considered to be a secondary effect, the main reason the sky is dark at night is because the universe is of a finite age and so only a finite number of stars contribute to the intensity of light at night. Any other stars that may exist are beyond the cosmic particle horizon.
(1) Swinburne University of Technology CD-ROM PowerPoint m17a01 slide 6.
(2) “Encyclopedia of Astrobiology, Astronomy & Spaceflight home page” Darling, D. http://www.daviddarling.info/encyclopedia/O/Olbers_Paradox.html
(3) Swinburne University of Technology CD-ROM PowerPoint m17a01 slide 7.
(4) Arpino, M. & Scardigli, F. “Inferences from the dark sky: Olbers’ paradox revisited (2002). http://xxx.lanl.gov/pdf/astro-ph/0007428
(4) Wikipedia Olbers’ Paradox Reference http://en.wikipedia.org/wiki/Olber%27s_paradox
(5) Lineweaver, C. A Younger Age for the Universe: Science, May 28, 1999, vol 284, 1503-1507
(6) Freedman, R. & Kaufmann, W. Universe, 6th Edition Freeman, 2002