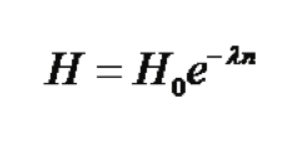Modelling Reality
“Modelling” is a term used to denote the process of representing some aspect of physical reality. In many cases, in many respects, the model itself becomes a part of physical reality. This is especially true when the model is, well, literally a physical model. Like a model airplane. When I was a student at school, if we were asked to “make a model” it would typically mean we’d be getting out the arts and crafts materials and making some kind of sculpture. If there was ever an occasion during a science lesson to “make a model” then it would be making something like a molecule from plasticine, toothpicks and Styrofoam spheres. It was almost never the case, as I recall, that we were asked “to model” something. Model was always a noun…never a verb.
Today in schools a more abstract type of modelling is de rigeur - by which I mean (ironically) the mathematical kind and not the fashionable sort involving runways and very thin people. Students of the physical sciences in senior school are encouraged to model this or that system. The model might be mathematical, it might be coded, or yes: it might even be built. The model is supposed to represent some actual system. The underlying lesson here is two fold: the student who is able to complete the model learns both about that process and appreciate that it is their model. They created it. So they - it is supposed - become aware that their model is not the thing itself which is represented and rather is only an imperfect simulacrum. In this way - whether physical or abstract - the model is analogous to synecdoche as a literary device. The model stands in for the whole without any pretence of being the whole.
For those outside physics, a quick example might suffice. The height of bounces of a ball, dropped once and allowed to bounce up and down until coming to rest exhibits a trend of what is known as exponential decay. There exists a mathematical formula for exponential decay. We can say “the exponential function models the bouncing of the ball”.
“Modelling” is a term used to denote the process of representing some aspect of physical reality. In many cases, in many respects, the model itself becomes a part of physical reality. This is especially true when the model is, well, literally a physical model. Like a model airplane. When I was a student at school, if we were asked to “make a model” it would typically mean we’d be getting out the arts and crafts materials and making some kind of sculpture. If there was ever an occasion during a science lesson to “make a model” then it would be making something like a molecule from plasticine, toothpicks and Styrofoam spheres. It was almost never the case, as I recall, that we were asked “to model” something. Model was always a noun…never a verb.
Today in schools a more abstract type of modelling is de rigeur - by which I mean (ironically) the mathematical kind and not the fashionable sort involving runways and very thin people. Students of the physical sciences in senior school are encouraged to model this or that system. The model might be mathematical, it might be coded, or yes: it might even be built. The model is supposed to represent some actual system. The underlying lesson here is two fold: the student who is able to complete the model learns both about that process and appreciate that it is their model. They created it. So they - it is supposed - become aware that their model is not the thing itself which is represented and rather is only an imperfect simulacrum. In this way - whether physical or abstract - the model is analogous to synecdoche as a literary device. The model stands in for the whole without any pretence of being the whole.
For those outside physics, a quick example might suffice. The height of bounces of a ball, dropped once and allowed to bounce up and down until coming to rest exhibits a trend of what is known as exponential decay. There exists a mathematical formula for exponential decay. We can say “the exponential function models the bouncing of the ball”.
Here Ho (read that as "H sub zero") is the initial height the ball is dropped from, while H is the height after n bounces. The Greek symbol λ (lambda) is a characteristic unique to the ball and surface (and other things) that governs how quickly the height of the ball “decays”. λ has to be measured: it is empirical.
Now should anyone subsequently perform an actual experiment to test that ball to find how high its 3rd bounce is - they will find that indeed the formula can do a remarkable job of predicting the behaviour of the ball, so long as λ has previously been found. But it is not perfect. It is not perfect because the mathematical model is not what physical reality ever does exactly. There exist “errors” when we attempt to measure reality - what are also called “uncertainties”. The uncertainties arise because the measurement of λ in the first place required the use of some measuring device (like a ruler) and it was not infinitely precise. And measuring the 3rd bounce likewise required an imperfect measuring device (and imperfect operator). And between when λ was first measured and the 3rd bounce test conducted, time has passed and conditions may have changed in the ball and the environment where the experiment is being conducted. And just plain old human error can creep into any part of science any time. Error is the normal state of things.
There are ways to correct some known errors. If we could conduct the investigation of “how close the mathematical formula models physical reality” in an environment without air it might work better. But no experiment in the real world, no matter how precise, will ever be able to show zero deviation from the model (in part local gravity actually varies in small amounts - we know this from geophysics, and no vacuum can ever be perfect and those are just two things over which we have no control but which may have an affect on any real world experiment.) In short: there is always a distance between the principle (which is what the model captures) and practice (which is what any experiment involving real balls and surfaces amounts to).
The mathematical formula in this case constitutes the model, and is regarded as some kind of ideal. It is not an actual physical thing. It is an abstraction purporting to represent an actual physical thing. Should anyone wish to engage in the bizarre attempt to replicate in physical reality how well the more general model works for “objects dropped from a height to the ground” then there would be better and worse ways to do this.
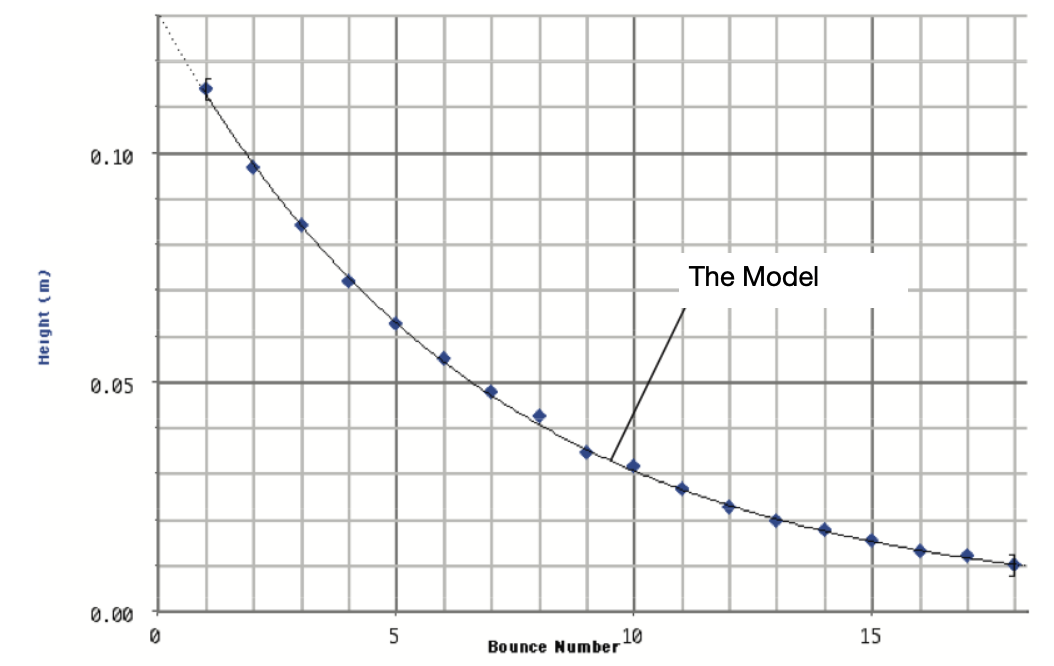
One terrible way to do this would be to drop a bowling ball into a puddle of mud. The ball would fall and splat creating a large crater, a great deal of mess and no bouncing. λ could not be measured. On the other hand, conducted in a vacuum, a metal ball bearing dropped onto a hard metallic surface will bounce and bounce and each bounce would be lower than before. A graph of such an experiment would look like that below.
Now should anyone subsequently perform an actual experiment to test that ball to find how high its 3rd bounce is - they will find that indeed the formula can do a remarkable job of predicting the behaviour of the ball, so long as λ has previously been found. But it is not perfect. It is not perfect because the mathematical model is not what physical reality ever does exactly. There exist “errors” when we attempt to measure reality - what are also called “uncertainties”. The uncertainties arise because the measurement of λ in the first place required the use of some measuring device (like a ruler) and it was not infinitely precise. And measuring the 3rd bounce likewise required an imperfect measuring device (and imperfect operator). And between when λ was first measured and the 3rd bounce test conducted, time has passed and conditions may have changed in the ball and the environment where the experiment is being conducted. And just plain old human error can creep into any part of science any time. Error is the normal state of things.
There are ways to correct some known errors. If we could conduct the investigation of “how close the mathematical formula models physical reality” in an environment without air it might work better. But no experiment in the real world, no matter how precise, will ever be able to show zero deviation from the model (in part local gravity actually varies in small amounts - we know this from geophysics, and no vacuum can ever be perfect and those are just two things over which we have no control but which may have an affect on any real world experiment.) In short: there is always a distance between the principle (which is what the model captures) and practice (which is what any experiment involving real balls and surfaces amounts to).
The mathematical formula in this case constitutes the model, and is regarded as some kind of ideal. It is not an actual physical thing. It is an abstraction purporting to represent an actual physical thing. Should anyone wish to engage in the bizarre attempt to replicate in physical reality how well the more general model works for “objects dropped from a height to the ground” then there would be better and worse ways to do this.
One terrible way to do this would be to drop a bowling ball into a puddle of mud. The ball would fall and splat creating a large crater, a great deal of mess and no bouncing. λ could not be measured. On the other hand, conducted in a vacuum, a metal ball bearing dropped onto a hard metallic surface will bounce and bounce and each bounce would be lower than before. A graph of such an experiment would look like that below.
Here the model and the real data match. The model well represents the data. The model is not entirely useless as an ideal form of the data.
Now, of course, no one much bothers to do things like this (the idiosyncrasies of school science syllabi aside). No one is attempting to force data to match a model (again, putting aside idiosyncratic and recent concerns about media fights over curve flattening and epidemiology). This is rather “back to front” to some extent. Actual modelling is about having the model match the data rather than trying to force things in the other direction. The purpose of a model in science is to constrain aspects of a theory so that useful interpolations (and sometimes attempts at extrapolations) might be made. This enables real world problem solving. Aeronautical engineering is one such field where highly experimental aircraft can be designed almost entirely in the abstract and actual problems solved based on well known models of fluid dynamics (how air moves) given wing and engine designs. Many trials can be conducted “in theory” as a wing design interpolated between two extremes known to perform well is put through its paces. Costs (and lives) are saved so that only in the very final stage is the experimental craft actually built and then carefully tested in the real world. And after that? The model is updated again with any new information from the real world.
The model, in that sense, is an abstract idealisation we have invented to capture some portion of physical reality - always imperfectly because the real world is infinitely complex and impossible to model perfectly. Not least because we are in it and we humans create knowledge: a process which itself defies modelling precisely because as David Deutsch has observed to predict the creation of future knowledge of some later time would be to have that knowledge now. A logical contradiction. As he wrote in “The Beginning of Infinity”, p 193
“The most important of all limitations on knowledge-creation is that we cannot prophesy: we cannot predict the content of ideas yet to be created, or their effects. This limitation is not only consistent with the unlimited growth of knowledge, it is entailed by it…”
Scientific theories are abstractions which only imperfectly capture physical reality. But if the physical world is “out there” and known only imperfectly how can imperfectly known abstractions ever be used to represent imperfectly understood physical reality in a reliable way? Moreover how can the world of abstractions - especially moral abstractions - ever hope to serve as some kind of source of ideals for the physical world we actually inhabit?
But any model is an ideal. And all ideals are abstractions. There is a to-ing and fro-ing between these things that leads to confusion in both morality and science. Morality is a domain where we seek to (imperfectly perhaps) meet abstract ideals by encouraging physical actions in the real world. By choosing this or that action to transform what is into what could (indeed should) be. In the real world of moral concerns we always find errors and imperfections. By what standard do we find errors? Places where we fail to live up to the ideals we have some knowledge of.
Yet in science the actual real world is, in a sense, what is actually true and perfect: where *the ideal is the imperfection* and the source of errors. The actual laws of physics of which we only have partial knowledge are in some sense ontologically perfect. They simply are as is physical reality itself. But our knowledge of them - contains imperfections. What can possibly happen - all those things in physical reality that really can happen - is a “perfect” set. It simply is what it is. But, again, our knowledge of what can possibly happen is an imperfect representation of that ideal
So in physics we have this idea of using mathematical ideals - abstractions - to model physical reality. This prompted Eugene Wigner's famous paper exploring "The Unreasonable Effectiveness of Mathematics in the Natural Sciences" an issue over which I shall skip. I am more concerned now with how the interplay between the abstract and physical works in the other direction. Namely how we attempt to organise physical reality - in terms of the organisation of our societies or even our personal lives in such a way as to more perfectly emulate the abstract ideal. So rather than the abstract being used to try to approximate the physical, it is in some sense we creative humans are trying to use the physical to more faithfully capture some abstract ideal. There is perfect freedom, or at least "ideal freedom" or "the best kind of freedom that humans could be expected to have" and we are reorganising ourselves around such an idea, or ideal - along with many others, often at odds. How does this work? Onto part 3 -->
Now, of course, no one much bothers to do things like this (the idiosyncrasies of school science syllabi aside). No one is attempting to force data to match a model (again, putting aside idiosyncratic and recent concerns about media fights over curve flattening and epidemiology). This is rather “back to front” to some extent. Actual modelling is about having the model match the data rather than trying to force things in the other direction. The purpose of a model in science is to constrain aspects of a theory so that useful interpolations (and sometimes attempts at extrapolations) might be made. This enables real world problem solving. Aeronautical engineering is one such field where highly experimental aircraft can be designed almost entirely in the abstract and actual problems solved based on well known models of fluid dynamics (how air moves) given wing and engine designs. Many trials can be conducted “in theory” as a wing design interpolated between two extremes known to perform well is put through its paces. Costs (and lives) are saved so that only in the very final stage is the experimental craft actually built and then carefully tested in the real world. And after that? The model is updated again with any new information from the real world.
The model, in that sense, is an abstract idealisation we have invented to capture some portion of physical reality - always imperfectly because the real world is infinitely complex and impossible to model perfectly. Not least because we are in it and we humans create knowledge: a process which itself defies modelling precisely because as David Deutsch has observed to predict the creation of future knowledge of some later time would be to have that knowledge now. A logical contradiction. As he wrote in “The Beginning of Infinity”, p 193
“The most important of all limitations on knowledge-creation is that we cannot prophesy: we cannot predict the content of ideas yet to be created, or their effects. This limitation is not only consistent with the unlimited growth of knowledge, it is entailed by it…”
Scientific theories are abstractions which only imperfectly capture physical reality. But if the physical world is “out there” and known only imperfectly how can imperfectly known abstractions ever be used to represent imperfectly understood physical reality in a reliable way? Moreover how can the world of abstractions - especially moral abstractions - ever hope to serve as some kind of source of ideals for the physical world we actually inhabit?
But any model is an ideal. And all ideals are abstractions. There is a to-ing and fro-ing between these things that leads to confusion in both morality and science. Morality is a domain where we seek to (imperfectly perhaps) meet abstract ideals by encouraging physical actions in the real world. By choosing this or that action to transform what is into what could (indeed should) be. In the real world of moral concerns we always find errors and imperfections. By what standard do we find errors? Places where we fail to live up to the ideals we have some knowledge of.
Yet in science the actual real world is, in a sense, what is actually true and perfect: where *the ideal is the imperfection* and the source of errors. The actual laws of physics of which we only have partial knowledge are in some sense ontologically perfect. They simply are as is physical reality itself. But our knowledge of them - contains imperfections. What can possibly happen - all those things in physical reality that really can happen - is a “perfect” set. It simply is what it is. But, again, our knowledge of what can possibly happen is an imperfect representation of that ideal
So in physics we have this idea of using mathematical ideals - abstractions - to model physical reality. This prompted Eugene Wigner's famous paper exploring "The Unreasonable Effectiveness of Mathematics in the Natural Sciences" an issue over which I shall skip. I am more concerned now with how the interplay between the abstract and physical works in the other direction. Namely how we attempt to organise physical reality - in terms of the organisation of our societies or even our personal lives in such a way as to more perfectly emulate the abstract ideal. So rather than the abstract being used to try to approximate the physical, it is in some sense we creative humans are trying to use the physical to more faithfully capture some abstract ideal. There is perfect freedom, or at least "ideal freedom" or "the best kind of freedom that humans could be expected to have" and we are reorganising ourselves around such an idea, or ideal - along with many others, often at odds. How does this work? Onto part 3 -->