This is a lightly edited transcript of ToKCast episode 111.
This can be an esoteric channel. But even for me this is an esoteric episode. I am not discussing a book or primarily a written piece at all. I am discussing a video lecture - by David Deutsch. It is, Ted talks aside, perhaps my favorite of David’s public talks. Now the reason I am doing this is that I just do not understand why it has not made more waves. I think it should get traction. So in this episode what I am doing is providing my take on David’s lecture. I emphasise that this is my take because as I like to say errors are my own and I expect to have made mistakes in misunderstanding what David has said in his lecture. Let me for a third time say again: these are my words. If I directly quote David I will say so - I don’t except where I’ve provided a literal clip of him speaking. I might get close at times to using his exact words but I’m labouring this point because I have added quite a bit of personally indulgent accoutrement we might say - hahah. Window dressing and emphasis and maybe some top spin just because I find it fun. So in other words this is all inspired by David’s talk - I certainly cannot say endorsed by him in any way.
If you want David’s words go directly to his lecture and double check there that what I say is representing what he says before - I don’t know - you decide to begin an email "Dear Professor Deutsch. I heard Brett Hall claim that you claim..." I am making no such claims. I am summarising ideas. And my summary is my own. Not David’s so - blame me. Now I’m also augmenting what I am saying with - primarily - a paper called “The Constructor theory of Probability” by Chiara Marletto. Now why am I bothering with this. Well the main reason is the main reason I do any of this: just because I want to. I find it fun to try and understand these ideas more deeply because at first they are always counter intuitive and then, after spending some time trying to understand them (rather than thinking “well that can’t work because X” or “that contradicts what I’ve known since primarily school so I’ll just reject that” and so on) - after taking the time to really digest them, meditate so to speak on the ideas then you end up thinking: how could it be otherwise? This is one of those cases and that process is fun. So that’s the first reason.
The second reason is that as some listeners are aware I’m in the midst of completing a series on Pinker’s book Rationality. Now in that book he devotes entire chapters to probability. Basically half the book is devoted to trying to explain how important probability theory is to rationality. Chapter 4 is called “Probability and Randomness”, 5 is “Beliefs and Evidence” - subtitled Bayesian Reasoning - which is just probability as applied to false epistemology and Chapter 6 is “Risk and Reward” - more probability and 7 is about decision theory using probability among other things and 9 is correlation and causation - all couched in terms of - you guessed it statistics and probability. Now I’m not just fixated on Pinker. Pinker as a thinker is not the issue. It is what his book Rationality represents - it is emblematic of the (underlined, boldfaced, italicised) THE way in which rationality-how to think-how to use reason - is seen by academia. It is how people are schooled in this insofar as they take an interest. And so that’s another reason I take an interest. I’m interested in misconceptions of that sort. The ones that are so deeply a part of culture they are formalised into courses and passed on generation after generation. Now admittedly there is an asymmetry lurking here. A book like Rationality is summarising what is the inherited wisdom (false though it is in places) of the expert class. It is not trying to illuminate a new and better way. The work of David Deutsch on the other hand is trying to do something different. It is the cutting edge of reason and science. So it’s unsurprising there is this conflict in places. Or sometimes just tension. I have not in my series so far done anything except encourage people to purchase Pinker’s book. Because I think it’s worth it. There is actually good stuff in there. But equally there are misconceptions. And they are misconceptions and exceedingly small number of people are aware are indeed misconceptions. Because what we’re going to talk about today is new - very new and to begin to understand it takes in our best epistemology as well as our best physics. In short it takes us taking realism seriously. We want to know what reality is really like. We don’t just want to make use of “useful fictions” as instruments to help us predict stuff. Sure, sometimes that is useful. The ideal gas law fails (for many reasons but among other things it assumes molecules have no forces between them) - but as a rough and ready estimate - it will do in many situations. As will any classical mechanics calculation of relative velocity (by ignoring relativistic effects) or any calculation of the distance to a star that doesn’t involve parallax. Science is replete with useful fiction. But none of them are good explanations once we know where exactly they’re false. They are not literal accounts of reality once we know they are false and how. In science we basically have once good explanations now known to be false and explanations yet to be shown false. As always, by way of illustration on that we have Newtonian gravity in the former category - a once good explanation but which we now know to be false. And in the latter we have General Relativity - a good explanation yet to be shown false.
Now that brings us to probability. Probability purports to be a scientific theory of a kind. It seeks to explain what is going on in the real physical world. So you take a so called fair coin and you toss it and the probability it comes up heads is, we are told, 1 in 2. So it’s the science of coin tosses. 50% will be heads and 50% will be tails. In the real world. Except of course it almost never is. Just try a large number of tosses. More than 100. It only approximately is 1 in every 2 or precisely 50% of the time. Indeed tossing a real coin 1000 times one should not expect precisely 500 heads. Only approximately 500 heads. But why? Well so the theory goes if you could toss it an infinite number of times then in the limit the number of heads would approach 50%. But then we’ve left the real world - awe’ve left science - because we can’t toss a coin an infinite number of times. Infinite coin tosses are not science. Actual scientific theories - actual theories of physics purport to be actual explanations of the real world - of what happens in the real world. The world being everything in physical existence. But if the actual explanation almost never actually accurately models what is going on, then what is going on? Well some might argue it’s true a priori - it’s an idealised mathematical model. Well - once more that’s not physics exactly then, is it? It’s pure mathematics. Again what is going on if not the precise probabilities suggested by the probability calculus for something as simply as a coin toss? Well - we’ll get there don’t worry. Before we do - just a few more remarks about probability and mathematics generally in terms of the broader sociological phenomena.
In the general educated populace, mathematical ability or knowledge or whatever you want to call it serves as a proxy for intelligence - according to some anyway. But in academia itself this often isn’t enough. You do see what appears to be an academic litmus test used on fellow members of the intelligentsia and that litmus test isn’t as broad as mathematical proficiency in general. It’s statistics and probability. It’s not: how good were your calculus scores? Or how far along in geometry did you get? Have you completed any topology courses? No the measure of mathematical proficiency often is probability and statistics. You see it: iconoclasts on social media - twitter is where it’s most obvious - one great mind berating another for not knowing enough probability or not having a good enough grip of it or having bad intuitions on that front - the probability front.
And haven’t we all felt chastised at one point or another by some media outlet when each time a terror attack happens, some pundit has to point out you’ve more chance of being hit by lightning than being blown up by a Jihadi’s bomb. “We just have bad intuitions about risk” we are told. Of course never mind that terrorist bombs going off have behind them sets of bad ideas while lightning strikes are not so motivated. There’s the matter of intent to contend with and intents can be changed which makes a world of difference in these cases. They are not the same kind of thing because mitigating them does not come down to the same kind of thing precisely. So of course that talk of comparative risk when it comes to terror incidents versus plain old tragic accidents is to avoid any discussion about the causes and perpetrators of terror attacks. Motivated reasoning some might call it - or holding certain ideas immune from criticism might say others.
And just on that - I think that example contains within it so much information that is readily portable to so many other examples where probability is misused. The idea here is that with terrorism (or even with lightning strikes for that matter) there exist good explanations for why they happen and in many cases where (if not when) and to who and by who. That helps people assess risk and prepare for it and mitigate it. The information that you - an individual living in New York or London or Sydney have a 1 in 1.6 million chance of being killed by a terror attack is almost contentless. Not all New Yorkers, Londoners or Sydney Siders have the same risk. Some barely leave home compared to others who travel via underground public transport to high rise office blocks. Even then there exist differences between different places in the same city.
The idea that YOU have a 1 in 500,000 chance of dying of a lightning strike is contentless too. It doesn’t help. However knowing not to be outside during thunderstorms carrying umbrellas or standing on the roof of a high rise - well those things do reduce your risk. The statistic of 1 in 500,000 death each year for the last 10 years were lightning strikes is not a probability of your future chance of death. If it comforts you maybe, if you knew nothing else, you’d think - that’s almost zero so who cares about flying a kite in the park during a thunderstorm. By the way these statistics on terror and lightning strikes are from the CDC where you can look up all sorts of chances of dying. But again YOU might not be typical.
There are many interpretations of probability. It’s rather like interpretations of quantum theory - or so called interpretations of quantum theory. And here like there I am not interested in refuting all the false claims - false interpretations - in either case. I just want to summarise a realistic conception of - in this case - probability. When I say realistic what I mean is: actually conforms to what we know of physics. Physics constrains what we can know of mathematics and when it comes to probability - people want to apply it to the real, physical world. So let’s take that seriously. Can we do this? To what extent? This is what David’s talk is about. You can find it online by searching YouTube with the key words David Deutsch probability. Now the talk is called Physics without Probability - but I have always found that a little misleading because it is far more wide ranging than that. I’ll link to the talk itself in the descriptions to this podcast. It’s fair to ask: if that talk is there why am I talking about a talk? Well - again - just to unpack these very new ideas in different language. And maybe it will inspire some to go to the original source material.
Let’s begin. David Deutsch as listeners will know is a pioneer in quantum information theory. He’s interested in drilling down to the foundations. What are the absolute fundamentals of what we know that underlie everything else? This is ironic because David Deutsch is simultaneously someone who denies there are foundations. So he’s looking at foundations and denying they are there. Haha. Well not quite. What this all means is he looks at the deepest knowledge we have and tries to go deeper. He just does not think like so many others who work in this area or are interested in the philosophy of all this that once you have found the deepest knowledge HITHERTO that this is where progress stops. It’s rather the opposite. Anywhere at all is a place to make progress and he chooses digging ever deeper. Quantum computation went deeper than regular quantum theory or regular computation. And now generalising - or going deeper - than quantum computation - and David finds and creates constructor theory - his theory of physics that goes beyond “laws and initial conditions” - the way physics until now has always been done. And a consequence of Constructor theory is the notion that things either can or cannot happen. They do not probability happen. We’ll keep coming back to this notion. But the point for now is that constructor theory showed that probability can be removed from our vision of reality. This is not all it does but for our purposes today - this is what it does do.
Constructor theory is a mode of explanation - a new mode of explanation. Probability is a mode of explanation. Initial conditions and laws are modes of explanation. David lists some more here.
If you want David’s words go directly to his lecture and double check there that what I say is representing what he says before - I don’t know - you decide to begin an email "Dear Professor Deutsch. I heard Brett Hall claim that you claim..." I am making no such claims. I am summarising ideas. And my summary is my own. Not David’s so - blame me. Now I’m also augmenting what I am saying with - primarily - a paper called “The Constructor theory of Probability” by Chiara Marletto. Now why am I bothering with this. Well the main reason is the main reason I do any of this: just because I want to. I find it fun to try and understand these ideas more deeply because at first they are always counter intuitive and then, after spending some time trying to understand them (rather than thinking “well that can’t work because X” or “that contradicts what I’ve known since primarily school so I’ll just reject that” and so on) - after taking the time to really digest them, meditate so to speak on the ideas then you end up thinking: how could it be otherwise? This is one of those cases and that process is fun. So that’s the first reason.
The second reason is that as some listeners are aware I’m in the midst of completing a series on Pinker’s book Rationality. Now in that book he devotes entire chapters to probability. Basically half the book is devoted to trying to explain how important probability theory is to rationality. Chapter 4 is called “Probability and Randomness”, 5 is “Beliefs and Evidence” - subtitled Bayesian Reasoning - which is just probability as applied to false epistemology and Chapter 6 is “Risk and Reward” - more probability and 7 is about decision theory using probability among other things and 9 is correlation and causation - all couched in terms of - you guessed it statistics and probability. Now I’m not just fixated on Pinker. Pinker as a thinker is not the issue. It is what his book Rationality represents - it is emblematic of the (underlined, boldfaced, italicised) THE way in which rationality-how to think-how to use reason - is seen by academia. It is how people are schooled in this insofar as they take an interest. And so that’s another reason I take an interest. I’m interested in misconceptions of that sort. The ones that are so deeply a part of culture they are formalised into courses and passed on generation after generation. Now admittedly there is an asymmetry lurking here. A book like Rationality is summarising what is the inherited wisdom (false though it is in places) of the expert class. It is not trying to illuminate a new and better way. The work of David Deutsch on the other hand is trying to do something different. It is the cutting edge of reason and science. So it’s unsurprising there is this conflict in places. Or sometimes just tension. I have not in my series so far done anything except encourage people to purchase Pinker’s book. Because I think it’s worth it. There is actually good stuff in there. But equally there are misconceptions. And they are misconceptions and exceedingly small number of people are aware are indeed misconceptions. Because what we’re going to talk about today is new - very new and to begin to understand it takes in our best epistemology as well as our best physics. In short it takes us taking realism seriously. We want to know what reality is really like. We don’t just want to make use of “useful fictions” as instruments to help us predict stuff. Sure, sometimes that is useful. The ideal gas law fails (for many reasons but among other things it assumes molecules have no forces between them) - but as a rough and ready estimate - it will do in many situations. As will any classical mechanics calculation of relative velocity (by ignoring relativistic effects) or any calculation of the distance to a star that doesn’t involve parallax. Science is replete with useful fiction. But none of them are good explanations once we know where exactly they’re false. They are not literal accounts of reality once we know they are false and how. In science we basically have once good explanations now known to be false and explanations yet to be shown false. As always, by way of illustration on that we have Newtonian gravity in the former category - a once good explanation but which we now know to be false. And in the latter we have General Relativity - a good explanation yet to be shown false.
Now that brings us to probability. Probability purports to be a scientific theory of a kind. It seeks to explain what is going on in the real physical world. So you take a so called fair coin and you toss it and the probability it comes up heads is, we are told, 1 in 2. So it’s the science of coin tosses. 50% will be heads and 50% will be tails. In the real world. Except of course it almost never is. Just try a large number of tosses. More than 100. It only approximately is 1 in every 2 or precisely 50% of the time. Indeed tossing a real coin 1000 times one should not expect precisely 500 heads. Only approximately 500 heads. But why? Well so the theory goes if you could toss it an infinite number of times then in the limit the number of heads would approach 50%. But then we’ve left the real world - awe’ve left science - because we can’t toss a coin an infinite number of times. Infinite coin tosses are not science. Actual scientific theories - actual theories of physics purport to be actual explanations of the real world - of what happens in the real world. The world being everything in physical existence. But if the actual explanation almost never actually accurately models what is going on, then what is going on? Well some might argue it’s true a priori - it’s an idealised mathematical model. Well - once more that’s not physics exactly then, is it? It’s pure mathematics. Again what is going on if not the precise probabilities suggested by the probability calculus for something as simply as a coin toss? Well - we’ll get there don’t worry. Before we do - just a few more remarks about probability and mathematics generally in terms of the broader sociological phenomena.
In the general educated populace, mathematical ability or knowledge or whatever you want to call it serves as a proxy for intelligence - according to some anyway. But in academia itself this often isn’t enough. You do see what appears to be an academic litmus test used on fellow members of the intelligentsia and that litmus test isn’t as broad as mathematical proficiency in general. It’s statistics and probability. It’s not: how good were your calculus scores? Or how far along in geometry did you get? Have you completed any topology courses? No the measure of mathematical proficiency often is probability and statistics. You see it: iconoclasts on social media - twitter is where it’s most obvious - one great mind berating another for not knowing enough probability or not having a good enough grip of it or having bad intuitions on that front - the probability front.
And haven’t we all felt chastised at one point or another by some media outlet when each time a terror attack happens, some pundit has to point out you’ve more chance of being hit by lightning than being blown up by a Jihadi’s bomb. “We just have bad intuitions about risk” we are told. Of course never mind that terrorist bombs going off have behind them sets of bad ideas while lightning strikes are not so motivated. There’s the matter of intent to contend with and intents can be changed which makes a world of difference in these cases. They are not the same kind of thing because mitigating them does not come down to the same kind of thing precisely. So of course that talk of comparative risk when it comes to terror incidents versus plain old tragic accidents is to avoid any discussion about the causes and perpetrators of terror attacks. Motivated reasoning some might call it - or holding certain ideas immune from criticism might say others.
And just on that - I think that example contains within it so much information that is readily portable to so many other examples where probability is misused. The idea here is that with terrorism (or even with lightning strikes for that matter) there exist good explanations for why they happen and in many cases where (if not when) and to who and by who. That helps people assess risk and prepare for it and mitigate it. The information that you - an individual living in New York or London or Sydney have a 1 in 1.6 million chance of being killed by a terror attack is almost contentless. Not all New Yorkers, Londoners or Sydney Siders have the same risk. Some barely leave home compared to others who travel via underground public transport to high rise office blocks. Even then there exist differences between different places in the same city.
The idea that YOU have a 1 in 500,000 chance of dying of a lightning strike is contentless too. It doesn’t help. However knowing not to be outside during thunderstorms carrying umbrellas or standing on the roof of a high rise - well those things do reduce your risk. The statistic of 1 in 500,000 death each year for the last 10 years were lightning strikes is not a probability of your future chance of death. If it comforts you maybe, if you knew nothing else, you’d think - that’s almost zero so who cares about flying a kite in the park during a thunderstorm. By the way these statistics on terror and lightning strikes are from the CDC where you can look up all sorts of chances of dying. But again YOU might not be typical.
There are many interpretations of probability. It’s rather like interpretations of quantum theory - or so called interpretations of quantum theory. And here like there I am not interested in refuting all the false claims - false interpretations - in either case. I just want to summarise a realistic conception of - in this case - probability. When I say realistic what I mean is: actually conforms to what we know of physics. Physics constrains what we can know of mathematics and when it comes to probability - people want to apply it to the real, physical world. So let’s take that seriously. Can we do this? To what extent? This is what David’s talk is about. You can find it online by searching YouTube with the key words David Deutsch probability. Now the talk is called Physics without Probability - but I have always found that a little misleading because it is far more wide ranging than that. I’ll link to the talk itself in the descriptions to this podcast. It’s fair to ask: if that talk is there why am I talking about a talk? Well - again - just to unpack these very new ideas in different language. And maybe it will inspire some to go to the original source material.
Let’s begin. David Deutsch as listeners will know is a pioneer in quantum information theory. He’s interested in drilling down to the foundations. What are the absolute fundamentals of what we know that underlie everything else? This is ironic because David Deutsch is simultaneously someone who denies there are foundations. So he’s looking at foundations and denying they are there. Haha. Well not quite. What this all means is he looks at the deepest knowledge we have and tries to go deeper. He just does not think like so many others who work in this area or are interested in the philosophy of all this that once you have found the deepest knowledge HITHERTO that this is where progress stops. It’s rather the opposite. Anywhere at all is a place to make progress and he chooses digging ever deeper. Quantum computation went deeper than regular quantum theory or regular computation. And now generalising - or going deeper - than quantum computation - and David finds and creates constructor theory - his theory of physics that goes beyond “laws and initial conditions” - the way physics until now has always been done. And a consequence of Constructor theory is the notion that things either can or cannot happen. They do not probability happen. We’ll keep coming back to this notion. But the point for now is that constructor theory showed that probability can be removed from our vision of reality. This is not all it does but for our purposes today - this is what it does do.
Constructor theory is a mode of explanation - a new mode of explanation. Probability is a mode of explanation. Initial conditions and laws are modes of explanation. David lists some more here.
These modes are ways of explaining what happens in the world. Each of them purport to be about reality. Actually what’s physically going on and why. So today we’re looking carefully at what’s in red there. Can things in reality be predicted - which is in this case explained - by recourse to probability? We are taking this seriously and literally as a description of reality.
By the way Constructor theory seeks to go deeper than all of these existing modes of explanation - it will see any of them to the extent they are valid at all - to be approximations to it but false in the final analysis - it will explain why they superficially appeared to be plausible - why they appear to work in some narrow domain and why they end up failing. Explanation in the constructor theoretic mode is via the dichotomy between transformations that can be either possible or impossible.
By the way Constructor theory seeks to go deeper than all of these existing modes of explanation - it will see any of them to the extent they are valid at all - to be approximations to it but false in the final analysis - it will explain why they superficially appeared to be plausible - why they appear to work in some narrow domain and why they end up failing. Explanation in the constructor theoretic mode is via the dichotomy between transformations that can be either possible or impossible.
By the way possible here means - following Chiara’s paper - “a thing being ‘possible’ in this sense means that it could be performed with arbitrarily high accuracy – not that it will happen with non-zero probability."
An approximation is not a literal description of reality. It is closer to metaphor. Newtonian mechanics we know is no longer an actual description of reality. There is no force of gravity. There is no action at a distance. There is no universal time ticking away for all of the universe. Some of the very things referred to as existing by the theory do not. At best Newton’s mechanics is a low velocity, low mass approximation that can provide a much better than random guess estimation of some physical quantities under some conditions. Useful for building houses and aiming rockets and so on. But as soon as you’re near a massive star or moving closer to the speed of light, operating particle accelerators and so on it fails to work. Only relativity or in other circumstances quantum theory provide the actual answer without correction in physics because we can take them literally as descriptions of reality.
But probability is not like relativity or quantum theory. It is not accurate to the limits of our measuring devices. It does not survive all tests - we’ve already seen that. Real life experiments with flipping coins or rolling dice almost never match what the probability calculus says. They only approximately do. But if that’s not a falsification then, by that measure, Eddington’s test failed to falsify Newtonian gravity. Of course in that case we had two theories to choose between. Here, what are our choices? Well the choices are rationality - which includes relying on quantum theory as it realistically is where we discuss what actually happens in reality - and, apparently, probability which more about all those things that might have happened in reality but did not and the tiny proportion of things that did happen. Which is overkill when you think about it.
Probability is at best an approximation (although an approximation to what, we might wonder). In short: there is no place for probability at the foundations of physics. But David does not make the case against probability from constructor theory here. He does not need to because independent of constructor theory the world is not probabalistic.
That’s just an illusion.
Probability theory is like the flat earth theory. It’s useful perhaps (for gardening) - but if you are thinking about what the laws of nature are then false theories are an impediment to understanding reality.
Let’s say that again. If you are thinking about what the laws of nature are then false theories are an impediment to understanding reality.
Probability was invented by people in 16th century like Cardano who wanted to win in games of chance and this began the mathematical field known as game theory. Probability is supposed to be a mathematical model for the intuitive idea that things are “fair” like dice and card shuffling and so on. The originators of that theory did not think the physical objects literally had the properties of fairness and literal randomness. They seemed to understand that the perfect idealisation of dice and card shuffling were not like actual physical dice and card shuffling
Cardano and his contemporaries did not assume games of chance were stochastic processes. A stochastic process is a literally random one - one governed not by deterministic laws of physics as understood at that time (now this was before Newtonian) - and this pre-Newtonian idea being basically Aristotle’s - there were deterministic laws even if they were not always well understood.
Whatever the case, games of chance did not literally have the properties of actual randomness that the probability calculus requires. It would never have occurred to them - the creators of probability - to connect physics to probability because the former - physics - was deterministic - not random.
Probability was used because it was too strong. It assumed literal randomness where they thought things were perhaps seemingly only approximately so and in that sense probability is a mathematical trick. The reason game theory is possible at all was that its conclusions do not depend on physics in the real world in the end. The theory of probability in truth was about modelling human social behaviour of a specific kind (namely playing certain games). Playing cards, rolling dice, flipping coins - these are things people do for entertainment (perhaps to earn money) - they are not features of the natural environment outside human societies. This mathematical trick about human social games nonetheless has found applications in diverse fields as if it’s fundamental in them. Roughly in historic order David lists them as:
An approximation is not a literal description of reality. It is closer to metaphor. Newtonian mechanics we know is no longer an actual description of reality. There is no force of gravity. There is no action at a distance. There is no universal time ticking away for all of the universe. Some of the very things referred to as existing by the theory do not. At best Newton’s mechanics is a low velocity, low mass approximation that can provide a much better than random guess estimation of some physical quantities under some conditions. Useful for building houses and aiming rockets and so on. But as soon as you’re near a massive star or moving closer to the speed of light, operating particle accelerators and so on it fails to work. Only relativity or in other circumstances quantum theory provide the actual answer without correction in physics because we can take them literally as descriptions of reality.
But probability is not like relativity or quantum theory. It is not accurate to the limits of our measuring devices. It does not survive all tests - we’ve already seen that. Real life experiments with flipping coins or rolling dice almost never match what the probability calculus says. They only approximately do. But if that’s not a falsification then, by that measure, Eddington’s test failed to falsify Newtonian gravity. Of course in that case we had two theories to choose between. Here, what are our choices? Well the choices are rationality - which includes relying on quantum theory as it realistically is where we discuss what actually happens in reality - and, apparently, probability which more about all those things that might have happened in reality but did not and the tiny proportion of things that did happen. Which is overkill when you think about it.
Probability is at best an approximation (although an approximation to what, we might wonder). In short: there is no place for probability at the foundations of physics. But David does not make the case against probability from constructor theory here. He does not need to because independent of constructor theory the world is not probabalistic.
That’s just an illusion.
Probability theory is like the flat earth theory. It’s useful perhaps (for gardening) - but if you are thinking about what the laws of nature are then false theories are an impediment to understanding reality.
Let’s say that again. If you are thinking about what the laws of nature are then false theories are an impediment to understanding reality.
Probability was invented by people in 16th century like Cardano who wanted to win in games of chance and this began the mathematical field known as game theory. Probability is supposed to be a mathematical model for the intuitive idea that things are “fair” like dice and card shuffling and so on. The originators of that theory did not think the physical objects literally had the properties of fairness and literal randomness. They seemed to understand that the perfect idealisation of dice and card shuffling were not like actual physical dice and card shuffling
Cardano and his contemporaries did not assume games of chance were stochastic processes. A stochastic process is a literally random one - one governed not by deterministic laws of physics as understood at that time (now this was before Newtonian) - and this pre-Newtonian idea being basically Aristotle’s - there were deterministic laws even if they were not always well understood.
Whatever the case, games of chance did not literally have the properties of actual randomness that the probability calculus requires. It would never have occurred to them - the creators of probability - to connect physics to probability because the former - physics - was deterministic - not random.
Probability was used because it was too strong. It assumed literal randomness where they thought things were perhaps seemingly only approximately so and in that sense probability is a mathematical trick. The reason game theory is possible at all was that its conclusions do not depend on physics in the real world in the end. The theory of probability in truth was about modelling human social behaviour of a specific kind (namely playing certain games). Playing cards, rolling dice, flipping coins - these are things people do for entertainment (perhaps to earn money) - they are not features of the natural environment outside human societies. This mathematical trick about human social games nonetheless has found applications in diverse fields as if it’s fundamental in them. Roughly in historic order David lists them as:
Experimental error - systematic and random - we will come back to these.
Actuarial science - this is where we look at risk. The risk of an investment or return or the chance of disaster or whether and to what extent some customer is worth insuring or lending to.
Brownian motion - this was studied by Einstein in one of his first papers. It’s where you have particles suspended in a liquid - a colloid is an example - and those usually solid particles are jostled around in the liquid by the motion of the molecules - usually water molecules.
The motivation for removing probability from these areas is just like the motivation for removing the celestial sphere from cosmology and the force of gravity from physics (and everywhere else for that matter).
In the process we explain why it has been (and remains) a useful fiction. It can be useful to think of something as risky. But notice that the whole notion of risky often refers to something that never happens. You might put $100 through a poker machine each weekend and it might be described as risky - regardless of whether you consistently win or not. If you win time and time again then the word risky refers to the thing that never happened.
Assertions about probabilities do not refer to the physical world. Either a thing happens or not. Saying something is likely or probable to happen is not about the real world where things just happen. They don’t probably happen. They happen.
And it’s no good saying that because something happens frequently that this means it is probable. Because exactly what is the probability? Exactly equal to the frequency? How do you know? Is that an axiom? Why? Do you say it’s because it’s probably the case that frequencies equal probabilities?
If you toss a coin 1000 times and it comes up heads 492 times and tails 508 times - that’s a frequency. So do we say the probability of heads in that case is 492/1000 for the next 500 throws? Why is it 1/2? Is it just probably 1/2 because it’s approximately 1/2? Why is that the case? Is it 1/2 because a priori - by definition it’s 1/2. Ok - but then again that’s not science because our experiment just refuted the exact 1/2 claim. The 1/2 is a bad explanation because it’s almost never matched and we have no good reason why it’s not matched.
The thing is that frequencies in real life do not exactly equal the supposed ideal probabilities. And any run of frequencies should not be expected to be exactly replicated in real life. As David says:
“It’s no good saying they equal them approximately (consult his original talk for 1 minute beginning at 17:50)…”
So probabilities only equal frequencies in theory if we have an infinite sequence. But we don’t have access to infinite sequences of events like coin tosses. And any finite sequence is not equal to an infinite sequence and we only ever have finite sequences. And how can we know any finite sequence is a typical sequence? We can’t. We can only say we probably have a typical sequence. So we’re going in circles.
It could be that probability is merely about ignorance - subjective ignorance. It could all just be about beliefs for example and a lack of knowledge in the minds of people. It could be a very parochial set of heuristics about how human minds work that reaches into the real world in some way. Ok but what way? What connects those claims about our minds to the real world? What is the rule? (Apparently this is what Bayesianism is all about, perhaps).
David Lewis tried to do this through his so called “Principal Principle”
Actuarial science - this is where we look at risk. The risk of an investment or return or the chance of disaster or whether and to what extent some customer is worth insuring or lending to.
Brownian motion - this was studied by Einstein in one of his first papers. It’s where you have particles suspended in a liquid - a colloid is an example - and those usually solid particles are jostled around in the liquid by the motion of the molecules - usually water molecules.
The motivation for removing probability from these areas is just like the motivation for removing the celestial sphere from cosmology and the force of gravity from physics (and everywhere else for that matter).
In the process we explain why it has been (and remains) a useful fiction. It can be useful to think of something as risky. But notice that the whole notion of risky often refers to something that never happens. You might put $100 through a poker machine each weekend and it might be described as risky - regardless of whether you consistently win or not. If you win time and time again then the word risky refers to the thing that never happened.
Assertions about probabilities do not refer to the physical world. Either a thing happens or not. Saying something is likely or probable to happen is not about the real world where things just happen. They don’t probably happen. They happen.
And it’s no good saying that because something happens frequently that this means it is probable. Because exactly what is the probability? Exactly equal to the frequency? How do you know? Is that an axiom? Why? Do you say it’s because it’s probably the case that frequencies equal probabilities?
If you toss a coin 1000 times and it comes up heads 492 times and tails 508 times - that’s a frequency. So do we say the probability of heads in that case is 492/1000 for the next 500 throws? Why is it 1/2? Is it just probably 1/2 because it’s approximately 1/2? Why is that the case? Is it 1/2 because a priori - by definition it’s 1/2. Ok - but then again that’s not science because our experiment just refuted the exact 1/2 claim. The 1/2 is a bad explanation because it’s almost never matched and we have no good reason why it’s not matched.
The thing is that frequencies in real life do not exactly equal the supposed ideal probabilities. And any run of frequencies should not be expected to be exactly replicated in real life. As David says:
“It’s no good saying they equal them approximately (consult his original talk for 1 minute beginning at 17:50)…”
So probabilities only equal frequencies in theory if we have an infinite sequence. But we don’t have access to infinite sequences of events like coin tosses. And any finite sequence is not equal to an infinite sequence and we only ever have finite sequences. And how can we know any finite sequence is a typical sequence? We can’t. We can only say we probably have a typical sequence. So we’re going in circles.
It could be that probability is merely about ignorance - subjective ignorance. It could all just be about beliefs for example and a lack of knowledge in the minds of people. It could be a very parochial set of heuristics about how human minds work that reaches into the real world in some way. Ok but what way? What connects those claims about our minds to the real world? What is the rule? (Apparently this is what Bayesianism is all about, perhaps).
David Lewis tried to do this through his so called “Principal Principle”
But that too gives no explanation as to why rational people should or do believe it. You may as well say why rational people avoid black cats or ladders. It’s not physics.
If we are rational then in what way should I conform my credence to a physical probability? After all probably winning is not the same as winning. So do I make the bet or not? A rational person is interested in what really is the case or really is going to be the case - not what probably is the case. If I am told when buying a house with wooden foundations that there’s probably not a termite infestation that’s not the same as being told: there’s not a termite foundation. The rational thing to do is to employ an expert to check and correct if there is. Either there is or there isn’t. “In this area it’s very rare for there to be termites. 99.9% of houses are free of termites. The risk of termites is vanishingly small. You probably don’t have termites.” It really is like “luck is on your side”. Again: that’s not rational. What’s rational is to check. And correct. But what if it’s prohibitively expensive to check. Isn't there a reasonable case then to do a cost benefit analysis on the fact so few people have termites? Well is it rational to gamble? That depends. If I have all my life savings almost being thrown into a house - no, it’s not rational when one knows there exist termites that could reduce your investment to near zero. And if checking is prohibitively expensive then don’t buy.
Ah: but someone else took that gamble and won. Turns out there were no termites. Ok: but that’s still not rational. If you use the poker machine - the gambling machine and have a streak of wins - the fact you won doesn’t make you rational. We are interested in rationality and reality here. And anyways in real life - in the termite case - it’s not prohibitively expensive and insofar as that is a metaphor for other situations, there will be explanations that allow one to gain the knowledge needed to find out what the risk really is. As I will come to - risk assessment is about having good explanations. Not about what will probably happen. But what is known to happen and what we know about how to mitigate when the worst is a possibility.
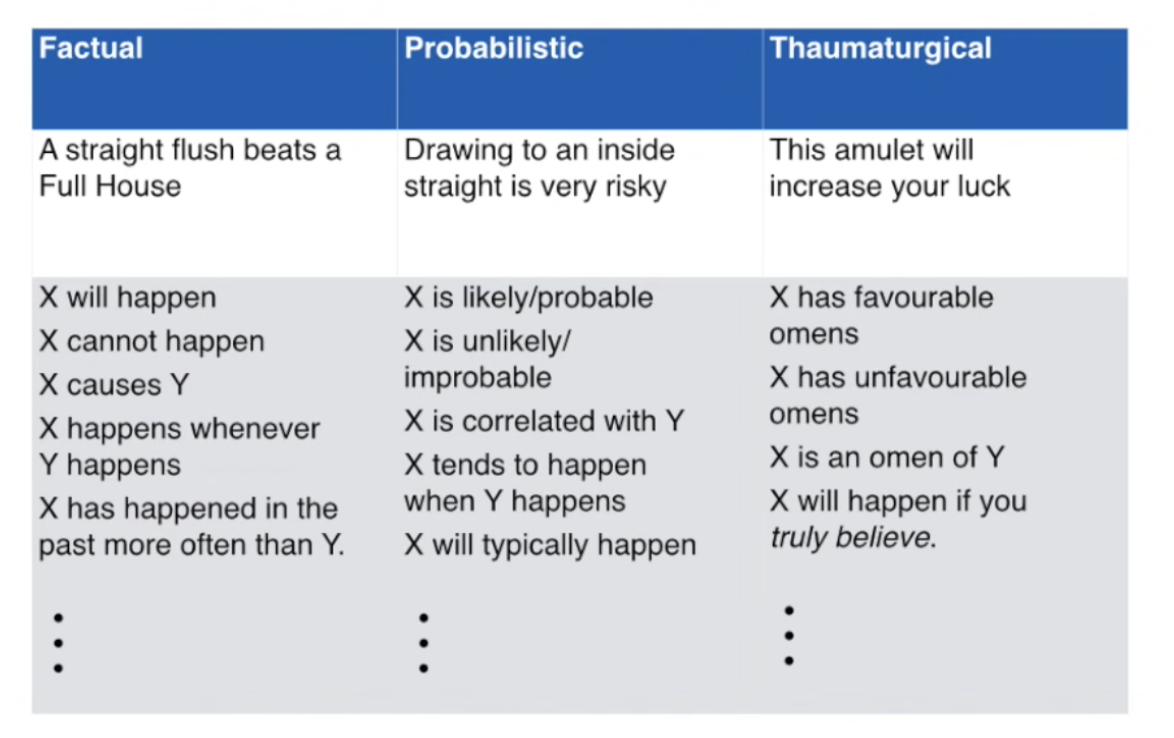
That hypothetical rational actor in probability scenarios is not the same as a real person. There are physical things and imaginary things. And they are not the same. To illuminate the way in which probability is disconnected from reality consider dividing statements about the world into factual ones and probabilistic ones. And by comparison magical ones. What makes the magical one worse than the probabilistic one?
(Pronunciation note: Thor-mat-er-logical)
If we are rational then in what way should I conform my credence to a physical probability? After all probably winning is not the same as winning. So do I make the bet or not? A rational person is interested in what really is the case or really is going to be the case - not what probably is the case. If I am told when buying a house with wooden foundations that there’s probably not a termite infestation that’s not the same as being told: there’s not a termite foundation. The rational thing to do is to employ an expert to check and correct if there is. Either there is or there isn’t. “In this area it’s very rare for there to be termites. 99.9% of houses are free of termites. The risk of termites is vanishingly small. You probably don’t have termites.” It really is like “luck is on your side”. Again: that’s not rational. What’s rational is to check. And correct. But what if it’s prohibitively expensive to check. Isn't there a reasonable case then to do a cost benefit analysis on the fact so few people have termites? Well is it rational to gamble? That depends. If I have all my life savings almost being thrown into a house - no, it’s not rational when one knows there exist termites that could reduce your investment to near zero. And if checking is prohibitively expensive then don’t buy.
Ah: but someone else took that gamble and won. Turns out there were no termites. Ok: but that’s still not rational. If you use the poker machine - the gambling machine and have a streak of wins - the fact you won doesn’t make you rational. We are interested in rationality and reality here. And anyways in real life - in the termite case - it’s not prohibitively expensive and insofar as that is a metaphor for other situations, there will be explanations that allow one to gain the knowledge needed to find out what the risk really is. As I will come to - risk assessment is about having good explanations. Not about what will probably happen. But what is known to happen and what we know about how to mitigate when the worst is a possibility.
That hypothetical rational actor in probability scenarios is not the same as a real person. There are physical things and imaginary things. And they are not the same. To illuminate the way in which probability is disconnected from reality consider dividing statements about the world into factual ones and probabilistic ones. And by comparison magical ones. What makes the magical one worse than the probabilistic one?
(Pronunciation note: Thor-mat-er-logical)
It is strange that the column about probability contains normative statements. Strange for science or physics. But you can’t get an ought from an is. Remember as David likes to say never mind so much being unable to derive an ought from an is. You cannot derive an is from an is either. That the sun is hot and produces light doesn’t not logically entail there is fusion reactions going on in the core. That explanation had to be conjectured. And that then goes to explain why the sun is hot and shines with light. It’s quite the other way around.
David goes on to summarise what a stochastic physical theory is all about - what it consists of. So if probability purports to be a part of reality then what we have are a factual part:
David goes on to summarise what a stochastic physical theory is all about - what it consists of. So if probability purports to be a part of reality then what we have are a factual part:
And this leads us to quantum theory because those other non-realistic models of quantum theory assert that the universe is stochastic. It’s wrong but how do they do it - especially given that the formalism of quantum theory does not explain in any way why some of the possibilities are actual and why some are never actualised. They remain only probable but never happen. How is that the case? Well they use
In my words - and more roughly speaking - the formalism of quantum theory describes observables - so physical properties of a system like the position of a particle - to be many valued or “not sharp”. And it does this because it really is not. Now when you measure the thing - say the position -you always get a sharp - basically single - value for whatever the observable is - like that position. The Born rule says that each possible value has a probability associated with it which is the square of the amplitude of the wave function. So probabilities are physical - they are a part of physics on this view - because they are the squares of how tall - the amplitude - of the wave function of the system.
That is the only way probability ever came into realistic objective science (or physics). Of course all of that assumes collapse of the wave function. And of course we know this does not happen. I say we know - I mean those who understand Everettian quantum theory or unitary quantum theory. Which is the way to say: the multiverse. The many worlds.
The way out of this is The Decision Theoretic Approach (sometimes “to the born rule” but that is circular).
That is the only way probability ever came into realistic objective science (or physics). Of course all of that assumes collapse of the wave function. And of course we know this does not happen. I say we know - I mean those who understand Everettian quantum theory or unitary quantum theory. Which is the way to say: the multiverse. The many worlds.
The way out of this is The Decision Theoretic Approach (sometimes “to the born rule” but that is circular).
By the way what this is saying here roughly speaking is that in 1/3 of the multiverse the value that appears is 2.7 and in the other 2/3rd it’s 5.9. Let’s not get into the details.
The decision theoretic approach is about what a rational person should do in a situation where the outcome is for them unpredictable given that probabilities are not actual. What Chiara says in her paper on probability is that “the decision-theoretic approach claims to explain the appearance of stochasticity in unitary quantum theory without invoking stochastic laws, rather as Darwin’s theory of evolution explains the appearance of design in biological adaptations without invoking a designer.”
Things are not actually random in the universe. Nothing actually random happens. It’s just that the laws are such that for any observer things are unpredictable because they are not able to have all the knowledge needed to know which universe their consciousness will be in after some measurement. Whether a quantum physicist or philosopher or whomever speaks in terms of actual probabilities given actual randomness or merely the appearance of randomness and the use of rationality makes no difference to what decision is made ultimately. It would be the same - it’s just that only one of them is realistic - actually is speaking about what actually happens in the real world.
David does spend some time on the technical details of quantum theory in the talk - but I won’t here. I will point the listener or viewer to my series on the multiverse if interested or to the original talk itself. Suffice it to say that alternatives to unitary quantum theory are not exactly parsimonious. They require lots more baggage and assumptions. Axioms if you like to try and produce a stochastic - or probabilistic theory of quantum reality. Now these axioms are not explanatory - so really should be ignored on that basis. They normally would be. We can reach the same conclusions without ever assuming collapse happens.
The decision theoretic approach is about what a rational person should do in a situation where the outcome is for them unpredictable given that probabilities are not actual. What Chiara says in her paper on probability is that “the decision-theoretic approach claims to explain the appearance of stochasticity in unitary quantum theory without invoking stochastic laws, rather as Darwin’s theory of evolution explains the appearance of design in biological adaptations without invoking a designer.”
Things are not actually random in the universe. Nothing actually random happens. It’s just that the laws are such that for any observer things are unpredictable because they are not able to have all the knowledge needed to know which universe their consciousness will be in after some measurement. Whether a quantum physicist or philosopher or whomever speaks in terms of actual probabilities given actual randomness or merely the appearance of randomness and the use of rationality makes no difference to what decision is made ultimately. It would be the same - it’s just that only one of them is realistic - actually is speaking about what actually happens in the real world.
David does spend some time on the technical details of quantum theory in the talk - but I won’t here. I will point the listener or viewer to my series on the multiverse if interested or to the original talk itself. Suffice it to say that alternatives to unitary quantum theory are not exactly parsimonious. They require lots more baggage and assumptions. Axioms if you like to try and produce a stochastic - or probabilistic theory of quantum reality. Now these axioms are not explanatory - so really should be ignored on that basis. They normally would be. We can reach the same conclusions without ever assuming collapse happens.
Realism is parsimonious. It is the simplest explanation. In the face of quantum unpredictability - and that’s unpredictability in the subjective sense of course - we can behave rationally. We can deploy reason. We can speak of having good explanations or not to inform our choices.
So there are no stochastic processes in nature according to quantum theory. Unitary quantum theory. The multiverse. What happens there happens according to the laws of quantum theory. So there are no credences because there are is no need for credences (credences being beliefs with numerical measures obeying the probability calculus). And just notice that idea of credence - a central part of Bayesian epistemology - is once more entirely subjectivist. It is about what is happening in particular minds - this notion of belief. It is not about objective knowledge - the solution to problems out there which either do work as solutions or do not (an objective criterion) - but rather, again: belief. Belief shares some qualities with “hope” or “fear” though the three are different of course. It is a private thought that something is going to happen - perhaps, or not. Or it could mean “really truly strongly think is true”. Whatever the case it is usually accompanied by powerful feelings. The religious share it with the superstitious who share it with the conspiratorial who, apparently, share it with the Bayesian’s who try to quantify it.
But knowledge is not about feelings. It is about what is the case and representing what is the case regardless of what people think is the case or how they feel about what is the case. There is knowledge without a knowing subject as Popper explains. And what happens in physics happens according to the laws of quantum theory. It does not say things probably happen because things do NOT probably happen. They happen. Or they do not happen.
And hence: we’ve dispensed with probability. Job done. :)
In this separation between collapse theories and unitary quantum theory we see that on the RHS we don’t merely derive we have explained as we don’t have to introduce unexplained postulates.
Returning to Cardano, in reality even games of chance are determined by quantum laws - because the laws of the universe are quantum. They govern everything. And again they are not literally described by the probability calculus. Decisions made based on probability theory in games of chance therefore are actually literally irrational (but then so is most gambling of course) - absent good explanations. Which can of course exist. Betting on games of chance seeks to make a prediction. But how? We are subjectively uncertain and the probability calculus does not hold anyway. General decision theory cannot take the probability calculus literally as a description of what is going on.
What is general decision theory, by the way? Well it’s just applying probability to - making decisions. Whatever the case rationality means being concerned with what we know and how to error correct what we know and allow all of that to inform our decisions. Not being concerned about what probably is the case. There is no probably. Again: things happen. They don’t probably happen.
And evolution does not require probability either as David explains in his talk because literally randomness is not needed. Random or not the theory works by selecting genes best suited to an environment. The theory doesn’t depend on true randomness. The essence is that the selection, not the mutations are systematic.
Chiara’s paper on the constructor theory of biology never evokes randomness.
None of this means the mathematical formalism of quantum theory is not sometimes useful. Of course it is. David is saying that the quantities called probabilities in that formalism never refer to any stocastic/random process in reality. Nor anything in rational minds. In physics or in minds thinking about physics.
Can there be a stochastic process in nature? Not as far as we know. As far as we know the universe is deterministic. Not random. Quantum statistical mechanics has entanglement and decoherence. It doesn’t need probability.
Experimental error seems to contain probability - one of the first uses after games of chance. But random errors - what are called random errors are not really random - they can be reduced without limit simply by repeating the measurement. In school or university science classes these random errors are things like well, you measure the length of something and then you measure it again and the two different measurements are slightly different because people aren’t perfect and parallax is the thing and so on. Or you might measure the mass of something on an analytical balance in chemistry class and one moment it’s 1.342g and the next it’s 1.344g and that’s because the wind blew or water was absorbed or some such. So you need to repeat and repeat again until you either get a reliable average or you know better what you’re doing and how to control your variables.
Systematic errors on the other hand are the other kind in science and they are are methodological. No amount of repeating will eliminate them. We cannot know what causes them in many cases - it’s ironic they are called systematic because no known system causes them.
Systematic errors are methodological errors because - well let me give a very simple school example. Students are asked to get into groups and measure the height of one of them. There might be 5 students, and another one whose height is measured. Tape measures, rulers, lasers - everything is tried. Lots of repeats. Averages are calculated with error bars produced.
(1.675±0.004)m
so the response comes back. So apparently the height is anywhere between 1.679m and 1.671m. The random error there gives the limits and the 0.004m there gives us our precision. But we might be entirely off - inaccurate because of systematic error. Now at the moment no one might be aware of what’s gone wrong in the system. They might never. But this sort of thing is par for the course in science. You cannot locate your error. But here I’ll just tell you the error. The student never took their shoes off. So really it’s not the height of the student that was ever found. It was height of student + height of shoe sole or some such. If you don’t know what’s gone wrong systematically - with the procedure - no amount of repeating the experiment will fix this. All the fancy statistics in the world and sigma confidence levels won’t help. Psychologists and astrophysicists alike take note. Repeating the experiment cannot make its conclusions more likely true or probably true. It’s about whether there is an error or not.
It doesn’t matter what a scientist believes about a theory - what credence they give it. Either the theory is true or not. Their beliefs about it are irrelevant. That subjectivist epistemology makes no difference to actual reason - objective knowledge.
Probability can be a metaphor or a technique for an approximation to make sense. But it should be an approximation to something. So if it is to inform decisions being made there should be an explanation rooted in a description of an actual physical world where events happen not probability happen.
It’s right and proper to expunge probability and randomness from the laws of physics to restore actual realism and rationality to the world. It’s a simplification and a unification and elimination of nonsense and…it’s true. The world is not probabilistic. For the umpteenth time here. Things happen. They don’t probably happen.
But instrumentalists will resist. What’s the benefit of this expunging if the formalism still works?
Well as David says "fundamental falsehoods don’t always rear up and bite you. You can believe in a flat earth and it might never affect your life and thinking. But belief in a flat earth theory could eventually conflict with a theory for avoiding asteroid strikes." Then you’ve got a problem to put it mildly. So we should be concerned about what is true and how to best understand reality.
Similarly you might very well continue to think probability theory is true or randomness is real and so on. You might even be able to invent quantum computers using this whole misconception. But because the Born rule contains misconceptions then you might not end up developing successors to quantum theory. Constructor theory for example is incompatible with probability.
If you assume that your garden is a flat bed then you can use the mathematics of flat surfaces. You don’t need to say “it’s an approximation to the flat earth” - it isn’t. There isn’t a flat earth for it to approximate to. So too here. We don’t assume that the probability calculus is an approximation to the underlying reality. It’s just some mathematics that can be useful.
Unpredictability can be modelled by randomness. Sometimes. But that still does not make the model correct. It doesn’t.
So that’s basically the content of David’s talk with lots of my peppering of my own reflections and top spin as I say. Now I just want to mention one other thing briefly and that’s about
So there are no stochastic processes in nature according to quantum theory. Unitary quantum theory. The multiverse. What happens there happens according to the laws of quantum theory. So there are no credences because there are is no need for credences (credences being beliefs with numerical measures obeying the probability calculus). And just notice that idea of credence - a central part of Bayesian epistemology - is once more entirely subjectivist. It is about what is happening in particular minds - this notion of belief. It is not about objective knowledge - the solution to problems out there which either do work as solutions or do not (an objective criterion) - but rather, again: belief. Belief shares some qualities with “hope” or “fear” though the three are different of course. It is a private thought that something is going to happen - perhaps, or not. Or it could mean “really truly strongly think is true”. Whatever the case it is usually accompanied by powerful feelings. The religious share it with the superstitious who share it with the conspiratorial who, apparently, share it with the Bayesian’s who try to quantify it.
But knowledge is not about feelings. It is about what is the case and representing what is the case regardless of what people think is the case or how they feel about what is the case. There is knowledge without a knowing subject as Popper explains. And what happens in physics happens according to the laws of quantum theory. It does not say things probably happen because things do NOT probably happen. They happen. Or they do not happen.
And hence: we’ve dispensed with probability. Job done. :)
In this separation between collapse theories and unitary quantum theory we see that on the RHS we don’t merely derive we have explained as we don’t have to introduce unexplained postulates.
Returning to Cardano, in reality even games of chance are determined by quantum laws - because the laws of the universe are quantum. They govern everything. And again they are not literally described by the probability calculus. Decisions made based on probability theory in games of chance therefore are actually literally irrational (but then so is most gambling of course) - absent good explanations. Which can of course exist. Betting on games of chance seeks to make a prediction. But how? We are subjectively uncertain and the probability calculus does not hold anyway. General decision theory cannot take the probability calculus literally as a description of what is going on.
What is general decision theory, by the way? Well it’s just applying probability to - making decisions. Whatever the case rationality means being concerned with what we know and how to error correct what we know and allow all of that to inform our decisions. Not being concerned about what probably is the case. There is no probably. Again: things happen. They don’t probably happen.
And evolution does not require probability either as David explains in his talk because literally randomness is not needed. Random or not the theory works by selecting genes best suited to an environment. The theory doesn’t depend on true randomness. The essence is that the selection, not the mutations are systematic.
Chiara’s paper on the constructor theory of biology never evokes randomness.
None of this means the mathematical formalism of quantum theory is not sometimes useful. Of course it is. David is saying that the quantities called probabilities in that formalism never refer to any stocastic/random process in reality. Nor anything in rational minds. In physics or in minds thinking about physics.
Can there be a stochastic process in nature? Not as far as we know. As far as we know the universe is deterministic. Not random. Quantum statistical mechanics has entanglement and decoherence. It doesn’t need probability.
Experimental error seems to contain probability - one of the first uses after games of chance. But random errors - what are called random errors are not really random - they can be reduced without limit simply by repeating the measurement. In school or university science classes these random errors are things like well, you measure the length of something and then you measure it again and the two different measurements are slightly different because people aren’t perfect and parallax is the thing and so on. Or you might measure the mass of something on an analytical balance in chemistry class and one moment it’s 1.342g and the next it’s 1.344g and that’s because the wind blew or water was absorbed or some such. So you need to repeat and repeat again until you either get a reliable average or you know better what you’re doing and how to control your variables.
Systematic errors on the other hand are the other kind in science and they are are methodological. No amount of repeating will eliminate them. We cannot know what causes them in many cases - it’s ironic they are called systematic because no known system causes them.
Systematic errors are methodological errors because - well let me give a very simple school example. Students are asked to get into groups and measure the height of one of them. There might be 5 students, and another one whose height is measured. Tape measures, rulers, lasers - everything is tried. Lots of repeats. Averages are calculated with error bars produced.
(1.675±0.004)m
so the response comes back. So apparently the height is anywhere between 1.679m and 1.671m. The random error there gives the limits and the 0.004m there gives us our precision. But we might be entirely off - inaccurate because of systematic error. Now at the moment no one might be aware of what’s gone wrong in the system. They might never. But this sort of thing is par for the course in science. You cannot locate your error. But here I’ll just tell you the error. The student never took their shoes off. So really it’s not the height of the student that was ever found. It was height of student + height of shoe sole or some such. If you don’t know what’s gone wrong systematically - with the procedure - no amount of repeating the experiment will fix this. All the fancy statistics in the world and sigma confidence levels won’t help. Psychologists and astrophysicists alike take note. Repeating the experiment cannot make its conclusions more likely true or probably true. It’s about whether there is an error or not.
It doesn’t matter what a scientist believes about a theory - what credence they give it. Either the theory is true or not. Their beliefs about it are irrelevant. That subjectivist epistemology makes no difference to actual reason - objective knowledge.
Probability can be a metaphor or a technique for an approximation to make sense. But it should be an approximation to something. So if it is to inform decisions being made there should be an explanation rooted in a description of an actual physical world where events happen not probability happen.
It’s right and proper to expunge probability and randomness from the laws of physics to restore actual realism and rationality to the world. It’s a simplification and a unification and elimination of nonsense and…it’s true. The world is not probabilistic. For the umpteenth time here. Things happen. They don’t probably happen.
But instrumentalists will resist. What’s the benefit of this expunging if the formalism still works?
Well as David says "fundamental falsehoods don’t always rear up and bite you. You can believe in a flat earth and it might never affect your life and thinking. But belief in a flat earth theory could eventually conflict with a theory for avoiding asteroid strikes." Then you’ve got a problem to put it mildly. So we should be concerned about what is true and how to best understand reality.
Similarly you might very well continue to think probability theory is true or randomness is real and so on. You might even be able to invent quantum computers using this whole misconception. But because the Born rule contains misconceptions then you might not end up developing successors to quantum theory. Constructor theory for example is incompatible with probability.
If you assume that your garden is a flat bed then you can use the mathematics of flat surfaces. You don’t need to say “it’s an approximation to the flat earth” - it isn’t. There isn’t a flat earth for it to approximate to. So too here. We don’t assume that the probability calculus is an approximation to the underlying reality. It’s just some mathematics that can be useful.
Unpredictability can be modelled by randomness. Sometimes. But that still does not make the model correct. It doesn’t.
So that’s basically the content of David’s talk with lots of my peppering of my own reflections and top spin as I say. Now I just want to mention one other thing briefly and that’s about
Risk Management
(This is not from David's talk. This is just Brett Hall riffing...)
As I say I’ve been asked about probability a number of times. A subset within this is the idea of risk mitigation. If we are saying something like probability is a scam - then how can we quantify risk and mitigate it? What is the rational approach?
There are a number of reasons to want to do this. Here are some:
Which companies to invest in?
Where to build a home?
How to assess likelihood of failure? For example mechanical failure of aircraft.
So there’s something that might be useful here that we could call a risk decision fork.
Consider the fact that:
Either you have a good explanation or not. In any circumstance. But let’s talk risk. Let’s specifically talk natural disasters and what to do about risk absent worrying about the probability of the risk - because that’s a fiction. We want to talk facts.
Here is my three pronged fork.
1. If you have a good explanation of the risk, its effects and where or when the bad event might happen: then prepare for the bad event.
2. If you lack a good explanation of whether and how a bad event is going to happen: then prepare for the worst when you can. Anything less is irresponsible and basically gambling.
3. If you have a good explanation that the bad event won’t happen only then can you act as if you know it won’t.
They are your options. And they are your only options.
If someone takes probability seriously and says the risk of the bad event is 10% or even 90% it’s no help whatsoever when it might be your home or life on the line. After all in either case the worst might happen tomorrow and effectively be consistent with that so-called prediction.
Here in Australia like most other places on Earth we’re plagued by natural disasters. Still, I’d prefer here than elsewhere because we tend not to get Earthquakes for the same reason we don’t have volcanoes. Luck of the continental draw. Now it’s not impossible to have Earthquakes but comparatively speaking this continent is stable. We get storms but rarely severe hurricane/typhoon like cyclones. They happen but to the north of the country.
What we do get are fires and floods. I’ll concentrate on the floods because they’ve been happening recently.
We live on a continent that is astonishingly flat. So when it rains it can flood. It does flood. It’s predictable. Yet people build homes, towns and whole cities on the flood plain. They know the flood will happen. We have good explanations of where floods happen. We know they happen frequently but like any weather event not exactly when. In this situation you know the flood will come. So you have to be ready for it. That’s the rational thing.
We have good explanations of floods and where they occur. Risk management says that in this situation if you choose to build in a place prone to floods you should expect your home to be flooded. So you cannot expect to be insured except for a lot of money and you should not expect the taxpayer to compensate you for choosing to live on a flood plain. No one will should stop you building on a flood plain. It’s cheap. So there’s risk and reward. But you can in theory build a house that will survive the flood.
At no point do you need to concern yourself with the fact it will probably flood. It won’t probably flood. It will flood. Period. So here’s what the decision fork says to do:
So: build your house on stilts. Or build on one of the rare hills. Construct your own hill. Or just construct the house such that when it does flood it’s not totally destroyed or it’s easy to repair - the electrical wiring is easy to get to or whatever. Either that or prepare by NOT living in the place prone to floods. This is all just logic and at no point do we need to gamble. We know what event will happen. Floods happen. We just don’t know exactly when. But again that’s not probably. We cannot say “probably next week” or “probably not next week”. We don’t know. Our best known explanation of floods in Australia also prohibits - for now - making precise predictions like that. All we can say is we don’t know. Which brings us to part 2. Because let’s say you buy the house but plan on living there for only 2 years. Maybe it won’t flood in the next two years. We do not have a good explanation of what floods will happen in two years. We lack a good explanation and so:
2. If you lack a good explanation of whether and how a bad event is going to happen: then prepare for the worst when you can. Anything less is irresponsible and basically gambling.
So here we say: we don’t know the flood will happen in two years but the rational thing to do is to prepare for it as if it will. As I say: anything less is irresponsible and amounts to replying on lucky charms.
Now you can avoid all this flood talk by living somewhere where we know it does not flood and have good reasons why it won’t flood. For example some places in Australia are at an altitude of over 100m and on steep inclines near the ocean. If you really wanted to avoid a flood then building on the side of sloping hill then no matter how hard the rain comes down it flows right by you into the sea and the ocean cannot possibly fill up with rain. You know enough science to know that even if all the ice in Antarctica and Greenland melted you’d still be safe because the maximum sea level rise is only 72m and you are up 100m so that gives you almost 30m of grace should even a tsunami strike. So in this case, with respect to flooding
3. If you have a good explanation that the bad event won’t happen only then can you act as if you know it won’t.
Of course you could still be hit by an asteroid. But in this case we’re in the situation of simply lacking good explanations - sufficient knowledge and wealth. Now in terms of large asteroids that might wipe out humanity well they are of a particular size such that our telescopes and present technology can detect them. In theory we’d have the wealth - the capacity to deflect them. But house destroying asteroids - we’re not there yet. But they are so infrequent that it’s a reasonable heuristic not to worry about the risk anymore than visiting Australia and being bitten by a funnel web spider.
In a very similar way when it comes to money the same principles hold. No one rational should want to invest in a company that will probably make money because no company probably makes money. Companies make money or they lose money. Of course some investors might want more insight that this - they want to know how much money will be made before they invest.
There are many people better placed than I to guide the rational investor through this maze but one thing that is clear is that probabilities are not a part of the picture. There is no way to know before hand what the future holds with any precision because the relevant factors depend upon human creativity - knowing how the product yet to be produced at scale works in the market - all that knowledge is yet to be created. The team of people coming together in that company to make things work they are yet to get to know each other under the conditions of success or temporarily failure and so on. So much knowledge is yet to be created and knowledge creation by its very nature is unpredictable. Inherently unpredictable as we say. So these kinds of predictions are not possible. But here is what is possible. You can either have some relevant and specific knowledge or you can lack it.
If you are an investor (or an employee or a founder or even the sole owner for that matter) you can know the product well. Or not. You don’t say “I’ve probably got a good understanding of what we are selling.” You do or you don’t. And the same goes for your employees - for the business. This is not to say you need to know about the intricate details of a person to know they are competent. You need to know that they have the relevant knowledge to get the job done. So you either have that knowledge or not. It’s again not a matter of probably having that knowledge. It’s black and white. In other words to keep this part relatively brief because I only want to make very broad brush strokes here - you either have a good explanation of why the business should succeed or not. If you lack a good explanation of what the business is, what the market is like and what the people working in that business are like and you invest anyway - well, you’re gambling. You might as well be putting the money through the casino where you only have a partial understanding of how the gaming machines work or exactly what the mathematics of roulette happens to be.
But if you do have good explanations you either do or don’t invest. In the case of the casino you know the whole thing is rigged on the side of the casino. Every game in the long run is set so that the odds are in the favour of the casino. So it’s not rational to play (modulo you’re just having fun with your friends and so on - but that’s different. It’s still irrational as a means of making money. It might be rational as a means of having fun so long as you expect to lose you money).
Ok - so to investing. There might also be a case to be made for having fun. For really taking the long shot bet. The young up and coming chemistry graduate comes to you with a plan for waterproof transparent paint that generates photovoltaic electricity - solar power. You don’t have the time to go into the details. You don’t have a good explanation. She seems genuine. She checks out online. She could be the next Elizabeth Holmes running a theranos type scam. But you are wealthy and she is only asking $200,000 and if she’s correct every building on Earth can be painted with transparent photovoltaic paint which during the day can power all the lights. Well maybe that qualifies as FUN. You won’t really miss the $200,000 and there’s something to be said for this particular innovator appearing to not want to damage their reputation. But it’s a gamble. You might just change the world of technology and engineering.
Now that case aside - simply having fun in the stock market rather than focussing directly on making money in all other cases you want to have knowledge. Knowledge of what actually is. Not because it can possibly guarantee what will be when it comes to success or failure in business but because knowledge is not a matter of probabilities. If you have a good explanation of the viability of the product, the hole in the market, lack of present competitors and knowledge of the skill and competence of the team then you do not need to be told by anyone else that your return on investment is probably going to be 50% over the next 5 years. Or probably 200%. Or any other number. Probably. The probably does not matter because there is no probably. Something is going to happen - businesses often fail but YOU personally know business (or at least you should if you’re asking this question) and so you have the knowledge of what to look for. None of this guarantees you won’t fail. You’re still fallible. You’ve taken all possible measures to avoid disasters you can foresee (you’ve not built the home on a flood plain) - but in business the equivalent of the asteroid or some other unforeseen natural disaster can still occur. But at no point have you needed to comfort yourself with the hope of good omens, protecting yourself with lucky charms or with the thought “I should probably be ok. This business is probably a good investment because the people are probably good at what they’re doing.”
There are no certainties in life and in human affairs (as much as global and cosmological events) what happens rather often is inherently unpredictable because what happens depends on human choices which themselves depends on human creativity. What people know - and what knowledge they create.
Things happen. They don’t probably happen. Knowledge is about good explanations of the world and can be instantiated in things other than minds. It’s not about beliefs and feelings. So Bayesianism is wrong. And rationality cannot possibly be about considerations of things that probably happen. The idea that it is resembles a sort of mysticism: contemplation of imaginary worlds. The worlds of the probable. But quantum theory tells us what can happen. And constructor theory is revealing a science of the possible and impossible and therefore how we can transform the world. It’s not that our decisions will probably change the world. They will. Or they won’t. We’ll either know how. Or we won’t. We’ll have the wealth to do what we want to. Or we won’t.
There’s no probably about it. And that doesn’t mean I’ll likely end the podcast here. I will. See you next time!
There are a number of reasons to want to do this. Here are some:
Which companies to invest in?
Where to build a home?
How to assess likelihood of failure? For example mechanical failure of aircraft.
So there’s something that might be useful here that we could call a risk decision fork.
Consider the fact that:
Either you have a good explanation or not. In any circumstance. But let’s talk risk. Let’s specifically talk natural disasters and what to do about risk absent worrying about the probability of the risk - because that’s a fiction. We want to talk facts.
Here is my three pronged fork.
1. If you have a good explanation of the risk, its effects and where or when the bad event might happen: then prepare for the bad event.
2. If you lack a good explanation of whether and how a bad event is going to happen: then prepare for the worst when you can. Anything less is irresponsible and basically gambling.
3. If you have a good explanation that the bad event won’t happen only then can you act as if you know it won’t.
They are your options. And they are your only options.
If someone takes probability seriously and says the risk of the bad event is 10% or even 90% it’s no help whatsoever when it might be your home or life on the line. After all in either case the worst might happen tomorrow and effectively be consistent with that so-called prediction.
Here in Australia like most other places on Earth we’re plagued by natural disasters. Still, I’d prefer here than elsewhere because we tend not to get Earthquakes for the same reason we don’t have volcanoes. Luck of the continental draw. Now it’s not impossible to have Earthquakes but comparatively speaking this continent is stable. We get storms but rarely severe hurricane/typhoon like cyclones. They happen but to the north of the country.
What we do get are fires and floods. I’ll concentrate on the floods because they’ve been happening recently.
We live on a continent that is astonishingly flat. So when it rains it can flood. It does flood. It’s predictable. Yet people build homes, towns and whole cities on the flood plain. They know the flood will happen. We have good explanations of where floods happen. We know they happen frequently but like any weather event not exactly when. In this situation you know the flood will come. So you have to be ready for it. That’s the rational thing.
We have good explanations of floods and where they occur. Risk management says that in this situation if you choose to build in a place prone to floods you should expect your home to be flooded. So you cannot expect to be insured except for a lot of money and you should not expect the taxpayer to compensate you for choosing to live on a flood plain. No one will should stop you building on a flood plain. It’s cheap. So there’s risk and reward. But you can in theory build a house that will survive the flood.
At no point do you need to concern yourself with the fact it will probably flood. It won’t probably flood. It will flood. Period. So here’s what the decision fork says to do:
- If you have a good explanation of the risk, its effects and where or when the bad event might happen: then prepare for the bad event.
So: build your house on stilts. Or build on one of the rare hills. Construct your own hill. Or just construct the house such that when it does flood it’s not totally destroyed or it’s easy to repair - the electrical wiring is easy to get to or whatever. Either that or prepare by NOT living in the place prone to floods. This is all just logic and at no point do we need to gamble. We know what event will happen. Floods happen. We just don’t know exactly when. But again that’s not probably. We cannot say “probably next week” or “probably not next week”. We don’t know. Our best known explanation of floods in Australia also prohibits - for now - making precise predictions like that. All we can say is we don’t know. Which brings us to part 2. Because let’s say you buy the house but plan on living there for only 2 years. Maybe it won’t flood in the next two years. We do not have a good explanation of what floods will happen in two years. We lack a good explanation and so:
2. If you lack a good explanation of whether and how a bad event is going to happen: then prepare for the worst when you can. Anything less is irresponsible and basically gambling.
So here we say: we don’t know the flood will happen in two years but the rational thing to do is to prepare for it as if it will. As I say: anything less is irresponsible and amounts to replying on lucky charms.
Now you can avoid all this flood talk by living somewhere where we know it does not flood and have good reasons why it won’t flood. For example some places in Australia are at an altitude of over 100m and on steep inclines near the ocean. If you really wanted to avoid a flood then building on the side of sloping hill then no matter how hard the rain comes down it flows right by you into the sea and the ocean cannot possibly fill up with rain. You know enough science to know that even if all the ice in Antarctica and Greenland melted you’d still be safe because the maximum sea level rise is only 72m and you are up 100m so that gives you almost 30m of grace should even a tsunami strike. So in this case, with respect to flooding
3. If you have a good explanation that the bad event won’t happen only then can you act as if you know it won’t.
Of course you could still be hit by an asteroid. But in this case we’re in the situation of simply lacking good explanations - sufficient knowledge and wealth. Now in terms of large asteroids that might wipe out humanity well they are of a particular size such that our telescopes and present technology can detect them. In theory we’d have the wealth - the capacity to deflect them. But house destroying asteroids - we’re not there yet. But they are so infrequent that it’s a reasonable heuristic not to worry about the risk anymore than visiting Australia and being bitten by a funnel web spider.
In a very similar way when it comes to money the same principles hold. No one rational should want to invest in a company that will probably make money because no company probably makes money. Companies make money or they lose money. Of course some investors might want more insight that this - they want to know how much money will be made before they invest.
There are many people better placed than I to guide the rational investor through this maze but one thing that is clear is that probabilities are not a part of the picture. There is no way to know before hand what the future holds with any precision because the relevant factors depend upon human creativity - knowing how the product yet to be produced at scale works in the market - all that knowledge is yet to be created. The team of people coming together in that company to make things work they are yet to get to know each other under the conditions of success or temporarily failure and so on. So much knowledge is yet to be created and knowledge creation by its very nature is unpredictable. Inherently unpredictable as we say. So these kinds of predictions are not possible. But here is what is possible. You can either have some relevant and specific knowledge or you can lack it.
If you are an investor (or an employee or a founder or even the sole owner for that matter) you can know the product well. Or not. You don’t say “I’ve probably got a good understanding of what we are selling.” You do or you don’t. And the same goes for your employees - for the business. This is not to say you need to know about the intricate details of a person to know they are competent. You need to know that they have the relevant knowledge to get the job done. So you either have that knowledge or not. It’s again not a matter of probably having that knowledge. It’s black and white. In other words to keep this part relatively brief because I only want to make very broad brush strokes here - you either have a good explanation of why the business should succeed or not. If you lack a good explanation of what the business is, what the market is like and what the people working in that business are like and you invest anyway - well, you’re gambling. You might as well be putting the money through the casino where you only have a partial understanding of how the gaming machines work or exactly what the mathematics of roulette happens to be.
But if you do have good explanations you either do or don’t invest. In the case of the casino you know the whole thing is rigged on the side of the casino. Every game in the long run is set so that the odds are in the favour of the casino. So it’s not rational to play (modulo you’re just having fun with your friends and so on - but that’s different. It’s still irrational as a means of making money. It might be rational as a means of having fun so long as you expect to lose you money).
Ok - so to investing. There might also be a case to be made for having fun. For really taking the long shot bet. The young up and coming chemistry graduate comes to you with a plan for waterproof transparent paint that generates photovoltaic electricity - solar power. You don’t have the time to go into the details. You don’t have a good explanation. She seems genuine. She checks out online. She could be the next Elizabeth Holmes running a theranos type scam. But you are wealthy and she is only asking $200,000 and if she’s correct every building on Earth can be painted with transparent photovoltaic paint which during the day can power all the lights. Well maybe that qualifies as FUN. You won’t really miss the $200,000 and there’s something to be said for this particular innovator appearing to not want to damage their reputation. But it’s a gamble. You might just change the world of technology and engineering.
Now that case aside - simply having fun in the stock market rather than focussing directly on making money in all other cases you want to have knowledge. Knowledge of what actually is. Not because it can possibly guarantee what will be when it comes to success or failure in business but because knowledge is not a matter of probabilities. If you have a good explanation of the viability of the product, the hole in the market, lack of present competitors and knowledge of the skill and competence of the team then you do not need to be told by anyone else that your return on investment is probably going to be 50% over the next 5 years. Or probably 200%. Or any other number. Probably. The probably does not matter because there is no probably. Something is going to happen - businesses often fail but YOU personally know business (or at least you should if you’re asking this question) and so you have the knowledge of what to look for. None of this guarantees you won’t fail. You’re still fallible. You’ve taken all possible measures to avoid disasters you can foresee (you’ve not built the home on a flood plain) - but in business the equivalent of the asteroid or some other unforeseen natural disaster can still occur. But at no point have you needed to comfort yourself with the hope of good omens, protecting yourself with lucky charms or with the thought “I should probably be ok. This business is probably a good investment because the people are probably good at what they’re doing.”
There are no certainties in life and in human affairs (as much as global and cosmological events) what happens rather often is inherently unpredictable because what happens depends on human choices which themselves depends on human creativity. What people know - and what knowledge they create.
Things happen. They don’t probably happen. Knowledge is about good explanations of the world and can be instantiated in things other than minds. It’s not about beliefs and feelings. So Bayesianism is wrong. And rationality cannot possibly be about considerations of things that probably happen. The idea that it is resembles a sort of mysticism: contemplation of imaginary worlds. The worlds of the probable. But quantum theory tells us what can happen. And constructor theory is revealing a science of the possible and impossible and therefore how we can transform the world. It’s not that our decisions will probably change the world. They will. Or they won’t. We’ll either know how. Or we won’t. We’ll have the wealth to do what we want to. Or we won’t.
There’s no probably about it. And that doesn’t mean I’ll likely end the podcast here. I will. See you next time!