|
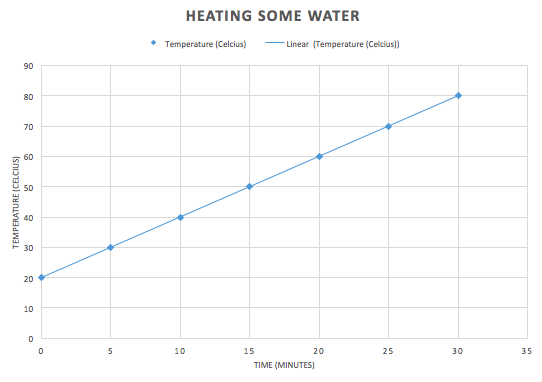
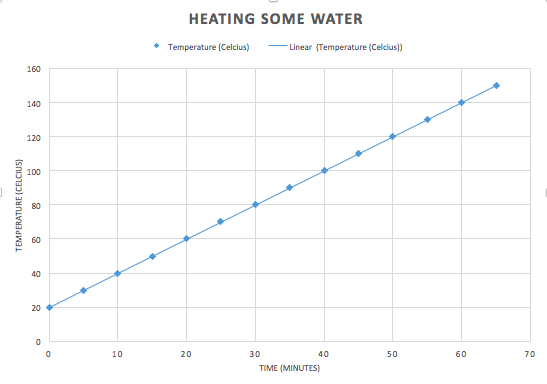
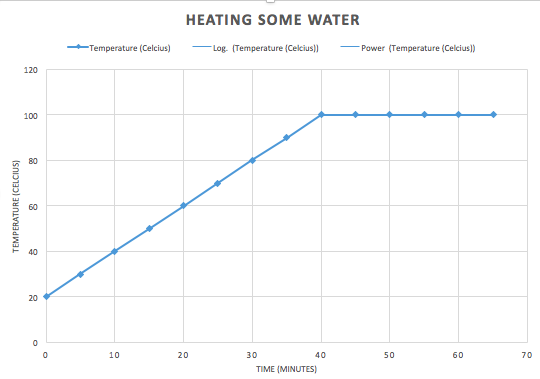
If you heat water on a stove and monitor the temperature as time passes - if the heat source is more or less constant and the environment is reasonably controlled (no strong breeze, say) then you will end up gathering data that looks something quite close to this (the details will, of course, depend on how powerful that heat source is and how much water you have) Say you keep heating the water. What happens next? What your answer is depends entirely on what knowledge you already have. If you genuinely think you do not know, you can guess. Note this: if you are in that position, it doesn't matter how "educated" you are. Your guess is as wild as anyone else's. "I have a PhD in Science" someone might say "But although I've no experience ever with this experiment, or anything like it, let me make an educated, expert guess..." Now that person's guess is no better than if they didn't have a PhD. Now there's a sense in which all knowledge is "guessed". But some guesses are made because they are derived from some existing theory. This is called a prediction. And if the theory being used is scientific we call such a conjecture a scientific prediction. Now a prediction is not a theory - a theory is an explanation - an account of why some phenomena happens in the way that it does. A prediction is where that general theory is taken and applied to a specific case. In science there is typically one "scientific theory" - namely the explanation - of any given phenomena. Sometimes there is no such theory (what is consciousness, for example?) and rarely there are competing theories (how do we resolve situations where quantum theory and general relativity conflict?) - often, like in this example of heating water - there is one explanation known. So...what happens next? If you're a person who thinks "induction" is a thing - guess now what happens next? If you already actually know what happens next, guess what someone who does not know would guess happens next. Many people think something like: well to make a prediction you "extrapolate", don't you? That's the rational thing to do. You have some data, so now continue the trend, right? It's a nice straight line - a "linear trend" so they say, so why not use what data we have and just continue the pattern? Why not indeed: Here, what is predicted is that the temperature of the water just continues to climb. We just follow the pattern previously and guess that the straight line just continues without limit. That might be called "pattern recognition" and is supposedly something like a sign of intelligence. A computer that can make that kind of guess might be well on the way to being smart like us, so we're told. In that context it can also be given the fancy title "Bayesian inference generation" (or something like this) and some people think that this is the kind of prediction that artificially intelligence machines are increasingly able to do. I criticise that line of thinking here: http://www.bretthall.org/superintelligence-4.html I should say: this guess seems quite reasonable. And it's even partially correct. From 80 to 90 degrees that next data point is correct. And so too is the one from 90 to 100 degrees. It is indeed very close to linear there. But anyone who has taken high school or even primary school science, or read a book about this, or seen the graph on the internet or perhaps even done this experiment themselves, knows this isn't true for values above 100 Celsius (yes, I'm assuming we're at sea level and the conditions are just such that "100 Celsius" is indeed the boiling point of water. Anyway, if you already know you might guess something strange happens at the boiling point. That "strange thing" is that as you heat beyond the boiling point (here assumed to be exactly 100 degrees Celsius) the temperature does not increase. It plateaus and will stay like that until all the water boils away (at which point your thermometer, if it keeps monitoring the temperature of the empty vessel will then start to increase in temperature again). Now could you predict this? Yes - if you already know the theory (or if you get wildly lucky). Most people who make this prediction either have seen it before (they know what actually happens) and they may even know a deeper explanation involving something about a thing called "latent heat" which is part of a general theory about how pure materials broadly speaking (like water) behave when they change state. The heating doesn't cause a temperature rise, but instead goes into breaking particle bonds and this takes energy not available to increase the kinetic energy of the particles (and hence the temperature). So even if you'd never had any experience with monitoring the temperature of water over time, if you knew about latent heat - and that water was a pure substance - you could make this prediction. You might not get the exact time and temperature when the graph flattens out correct, but you could at least make this prediction roughly speaking and far more accurately than the plain straight line "extrapolation from induction".
But absent that theory about latent heat that you already know you are just wildly guessing. And it wouldn't matter who you were. The thing about a guess (that's a prediction) and a guess (that's wild) is that in the former case you can provide some deeper-than-surface account of why you choose this over that. In the first prediction where you just continue the straight line (some people call this kind of thing "induction") well, you're just superficially assuming the pattern continues. But why? No reason. It just seems as though it should and perhaps you've heard the word "extrapolate" before? But you're guessing. You're actually creatively trying to come up with something reasonable. You're not using "induction" (but if you were, we've just shown it leads you straight into error) you are guessing: making a conjecture. In your mind you might think "the water gets to 100 then boils away getting hotter and hotter because - well what else could happen?). If you don't know, you just don't know. And your guess will be uncoupled from - in this case - actual science. Namely: the best known explanation that has been discovered. The second prediction is a prediction from a theory itself creatively conjectured some time in the past and tested over and again under many different conditions. It did not come from induction either. Many people over many years, working together, had to explain that matter was made of ever smaller particles that themselves were held together by forces and that energy was required to break the forces of attraction between these particles and that this caused changes of state. And this theory isn't contradicted by lots of other science - but instead is essential for progress in other areas too. But its development had nothing to do with collecting lots of data and then "extrapolating" to the "best hypothesis". If that was the case: we shouldn't expect any more accuracy than we do in that straight line graph above. Now people in hard sciences like chemistry and physics are well aware of this kind of thing. But strangely, when it comes to other areas it is almost a rule that to "extrapolate" is the very height of sophisticated data-informed, evidence-based reasoning. But we have seen that with even the most simple system we can imagine (heating water on a stove) extrapolation cannot work. So how can we possibly expect it to work when things are more complicated and with more variables? And yet doomsday prophesies about population www.bretthall.org/cosmological-economics.html are common and rest on how graphs monitoring the growth of people "suggest" or "imply" terrible things to come. But how can such a prediction be made on the basis of data alone? On the basis of data alone, liquid water would seem to continue to get ever hotter even after it boils. And if you are trying to program your robot to be ever more clever, it can only be clever like a person if it can make conjectures like a person. And as we have seen here: if it is required to only make guesses as a "Bayesian Inference Generator" then it will forever be restricted to just those things it has been programmed to be able to predict. It won't be able to genuinely create new knowledge because it is programmed not to be creative but rather to implement an uncreative extrapolation algorithm that pattern matches. This, by the way, is why some of us question the conclusions that psychologists (and related researchers) draw. They have lots of data and lots of models and even "predictions" from those models. But to us, their graphs often look like that first graph above: a very good set of data (excellent correlation coefficients (a measure of how closely the data matches the "model" (i.e: how closely the points sit on the line))) all very carefully collected and precisely reported on. But no explanation. The data leads to a model that is explanationless. It does not account for why that graph and not some other and it does not explain whether and how it might be wrong or how it might be just a small part of a much larger phenomena. Therefore attempts to draw conclusions using such a model are in truth "pure guesswork" and nothing like a "scientific prediction". Lots and lots of precise data is not what science is about - or else science would just be about those first two graphs. Science is about the deep explanations of the world - that accompany that 3rd graph. The purpose of additional data gathered is to rule out the second graph and its accompanying explanation (if there is one), with a complete accounting as to why it's false in terms of latent heat, and moreover allowing us to make an infinite number of predictions about not only water but all substances. And at no point did we ever need the chimera of "induction".
4 Comments
Sankar Mukherjee
7/17/2018 03:49:42 pm
Very thought provoking indeed. Do you have a solution in mind?
Reply
Brett
8/25/2018 05:44:39 am
Solution to?
Reply
Leave a Reply. |
Archives
December 2023
CriticismThe most valuable thing you can offer to an idea Categories |
 RSS Feed
RSS Feed